|
2011年中考第一轮复习教学案:第27课时 勾股定理与锐角三角函数
第27课时 勾股定理与锐角三角函数
一、中考知识点
1.测量的方法;2.勾股定理;3. 锐角三角函数的定义;4.特殊角的三角函数值;
5.直角三角形的性质.
二、中考课标要求
|
考点 |
课标要求 |
知识与技能目标 |
|
了解 |
理解 |
掌握 |
灵活应用 |
|
测量 |
掌握测量的方法 |
|
|
∨ |
∨ |
|
勾股定理 |
掌握勾股定理的推导过程 |
|
∨ |
∨ |
|
|
灵活应用勾股定理计算 |
|
|
∨ |
∨ |
|
锐角三角函数 |
了解锐角三角函数的概念 |
∨ |
|
|
∨ |
|
熟记特殊角的三角函数值 |
|
|
∨ |
∨ |
|
掌握直角三角形的性质 |
|
|
∨ |
∨ |
三、中考知识梳理
1.勾股定理
勾股定理的验证方法很多,用面积验证比较简捷.用面积法解题是一种重要的解题方法,在有距离或垂线段的条件的题目中运用面积法解题比较方便.
2.锐角三角函数的概念
锐角三角函数的概念应通过画图帮助分析,通过画图找出直角三角形中边、 角的关系,加深对概念的理解.
3.特殊角的三角函数值
对于特殊角的三角函数值,必须熟练准确地记住,记忆时可借助三角板上的直角三角形.
4.常联系的知识点
锐角三角函数常和三角形、四边形、相似形、圆、坐标系、一元二次方程结合命题。
四、中考题型例析
1.勾股定理
例1 (2004.黄冈)若直角三角形的三边长为2、4、x,则x的可能值有( ).
A.1个 B.2个 C.3个 D.4个
解析:本题没有说明4,x谁为斜边,故应分两种情况讨论.
答案:B.
2.锐角三角函数的定义
例2 (2004.南京)在△ABC中,∠C=90°,如果AB=2,BC=1,那么sinA的值是( ). A.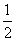 B. B. C. C. |

