|
2011年中考数学复习知识讲解+例题解析+强化训练
用函数的观点看方程(组)与不等式
◆知识讲解
1.一元一次方程、一元一次不等式及一次函数的关系
一次函数及其图像与一元一次方程及一元一次不等式有着密切的关系,函数y=ax+b(a≠0,a,b为常数)中,函数的值等于0时自变量x的值就是一元一次方程ax+b=0(a≠0)的解,所对应的坐标(-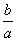 ,0)是直线y=ax+b与x轴的交点坐标,反过来也成立;直线y=ax+b在x轴的上方,也就是函数的值大于零,x的值是不等式ax+b>0(a≠0)的解;在x轴的下方也就是函数的值小于零,x的值是不等式ax+b<0(a≠0)的解. ,0)是直线y=ax+b与x轴的交点坐标,反过来也成立;直线y=ax+b在x轴的上方,也就是函数的值大于零,x的值是不等式ax+b>0(a≠0)的解;在x轴的下方也就是函数的值小于零,x的值是不等式ax+b<0(a≠0)的解.
2.坐标轴的函数表达式
函数关系式x=0的图像是y轴,反之,y轴可以用函数关系式x=0表示;函数关系式y=0的图像是x轴,反之,x轴可以用函数关系式y=0表示.
3.一次函数与二元一次方程组的关系
一般地,每个二元一次方程组,都对应着两个一次函数,于是也就是对应着两条直线,从“数”的角度看,解方程相当于考虑自变量为何值时两个函数的值相等,以及这两函数值是何值;从形的角度考虑,解方程组相当于确定两条直线的交点坐标,所以一次函数及其图像与二元一次方程组有着密切的联系.
4.两条直线的位置关系与二元一次方程组的解
(1)二元一次方程组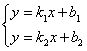 有唯一的解 有唯一的解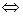 直线y=k1x+b1不平行于直线y=k2x+b2 直线y=k1x+b1不平行于直线y=k2x+b2 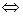 k1≠k2. k1≠k2.
(2)二元一次方程组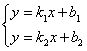 无解 无解 直线y=k1x+b1∥直线y=k2x+b2 直线y=k1x+b1∥直线y=k2x+b2  k1=k2,b1≠b2. k1=k2,b1≠b2.
(3)二元一次方程组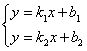 有无数多个解 有无数多个解 直线y=k1x+b1与y=k2x+b2重合 直线y=k1x+b1与y=k2x+b2重合 k1=k2,b1=b2. k1=k2,b1=b2. |

