|
第三单元 第17课时
二次函数与一元二次方程
知识点回顾:
知识点一:二次函数y=ax2+bx+c图象与一元二次方程ax2+bx+c=0的根的关系
一般地,二次函数y=ax2+bx+c图象与一元二次方程ax2+bx+c=0的根有如下关系:
1、如果二次函数y=ax2+bx+c图象与x轴有两个交点(m,0)、(n,0),那么一元二次方程ax2+bx+c=0有 实数根x1= ,x2= .
2、如果二次函数y=ax2+bx+c图象与x轴有一个交点(m,0),那么一元二次方程ax2+bx+c=0有 实数根x1=x2= 。
3、如果二次函数y=ax2+bx+c图象与x轴没有交点,那么一元二次方程ax2+bx+c=0
实数根。
例1:已知抛物线y=mx2+(3-2m)x+m-2(m≠0)与x轴有两个不同的交点.
(1)求m的取值范围;
(2)判断点P(1,1)是否在抛物线上;
同步测试:
1.(2008年湖北省咸宁市)抛物线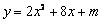 与 与 轴只有一个公共点,则 轴只有一个公共点,则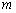 的值为 . 的值为 .
2.已知二次函数y=x2-4x+k+2与x轴有公共点,求k的取值范围.
知识点二:由一元二次方程ax2+bx+c=0的根的情况可以判断二次函数y=ax2+bx+c图象与x轴的交点个数。
1、当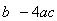 >0时,一元二次方程ax2+bx+c=0的根的情况是 ,此时二次函数y=ax2+bx+c图象与x轴有 交点; >0时,一元二次方程ax2+bx+c=0的根的情况是 ,此时二次函数y=ax2+bx+c图象与x轴有 交点;
2、当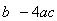 =0时,一元二次方程ax2+bx+c=0的根的情况是 ,此时二次函数y=ax2+bx+c图象与x轴有 交点; =0时,一元二次方程ax2+bx+c=0的根的情况是 ,此时二次函数y=ax2+bx+c图象与x轴有 交点; |

