|
第四单元第28课时
解直角三角形及其应用
知识点回顾
知识点1:解直角三角形
1、解直角三角形的类型:
根据求解的条件分类,利用边角关系可有如下基本基本类型及其解法:
(1)已知两边:
①两条直角边a、b.其解法:c=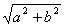 ,用tanA= ,求得∠A,∠B=90°-∠A. ,用tanA= ,求得∠A,∠B=90°-∠A.
②斜边和一条直角边c、a.其解法:b=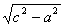 ,用sinA= ,求得∠A,∠B=90°-∠A. ,用sinA= ,求得∠A,∠B=90°-∠A.
(2)一边和一锐角:
①一条直角边a和锐角A:∠B=90°-∠A;用tanA=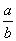 ,求得b= ;用sinA= ,求得b= ;用sinA=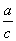 ,求得c= . ,求得c= .
②斜边c和锐角A:∠B=90°-∠A;用sianA=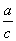 ,求得a= ;用cosA= ,求得a= ;用cosA=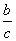 ,求得b= . ,求得b= .
2、解直角三角形的方法(口诀):
“有斜用弦,无斜用切;宁乘毋除,取原避中.”这两句话的意思是:当已知和求解中有斜边时,就用正弦或余弦;无斜边时,就用正切;当所求的元素既可用乘法又可用除法时,则用乘法,不用除法;既可用已知数据又可用中间数据求解时,则用原始数据,尽量避免用中间数据.
【友情提示】
⑴解题时方法要灵活,选择关系时尽量考虑用原始数据,减小误差;
⑵斜三角形问题可添加合适的辅助线转化为直角三角形问题。
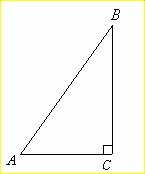 例1:(08年宁夏中考)如图,在△ 例1:(08年宁夏中考)如图,在△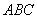 中,∠ 中,∠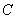 =90°,sin =90°,sin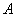 = =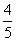 , ,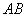 =15,求△ =15,求△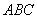 的周长和tan 的周长和tan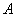 的值. 的值.
解析:应用直角三角形边角关系求出各边长, |

