|
-
代数综合题
Ⅰ、综合问题精讲:
代数综合题是指以代数知识为主的或以代数变形技巧为主的一类综合题.主要包括方程、函数、不等式等内容,用到的数学思想方法有化归思想、分类思想、数形结合思想以及代人法、待定系数法、配方法等.解代数综合题要注意归纳整理教材中的基础知识、基本技能、基本方法,要注意各知识点之间的联系和数学思想方法、解题技巧的灵活运用,要抓住题意,化整为零,层层深人,各个击破.注意知识间的横向联系,从而达到解决问题的目的.
Ⅱ、典型例题剖析
【例1】(2005,丽水,8分)已知关于x的一元二次方程x2-(k+1) x-6=0的一个根是2,求方程的另一根和k的值.
解:设方程的另一根为x1,由韦达定理:2 x1=-6,
∴ x1=-3.由韦达定理:-3+2= k+1,∴k=-2.
【例2】(2005,嘉峪关,7分)已知关于x的一元二次方程(k+4)x2+3x+k2-3k-4=0的一个根为0,求k的值.
解:把x=0代入这个方程,得k2-3k-4=0,解得k1=l,k2=-4.因为k+4≠0.所以k≠-4,所以k=l。
点拨:既然我们已经知道方程的一个根了,那么我们就可以将它代入原方程,这样就可以将解关于x的方程转化为解关于k的方程.从而求出b的解.但应注意需满足k+4的系数不能为0,即k≠-4。
【例3】(2005,自贡,5分)已对方程 2x2 +3x-l=0.求作一个二次方程,使它的两根分别是已知方程两根的倒数.
解:设2 x2 +3x-l=0的两根为x1、x2
则新方程的两根为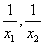 得 得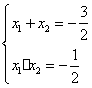
所以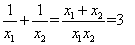 所以新方程为y2-3y-2=0· 所以新方程为y2-3y-2=0·
点拨:熟记一元二次方程根与系数的关系是非常必要的
【例4】(2005,内江,8分)某产品每件成本10元,试销阶段每件产品的日销售价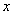 (元)与产品的日销售量 (元)与产品的日销售量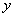 (件)之间的关系如下表: (件)之间的关系如下表:
|
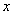 (元) (元)
|
15 |
20 |
25 |
30 |
… |
|
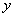 (件) (件)
|
25 |
20 |
15 |
10 |
… |
⑴在草稿纸上描点,观察点的颁布,建立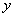 与 与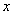 的恰当函数模型。 的恰当函数模型。
⑵要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
解:⑴经观察发现各点分布在一条直线上,
∴设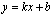 (k≠0) (k≠0) |

