数形结合

Ⅰ、专题精讲：

     数学家华罗庚说得好：“数形结合百般好，隔离分家万事休，几何代数统一体，永远联系莫分离”．几何图形的形象直观，便于理解，代数方法的一般性，解题过程的机械化，可操作性强，便于把握，因此数形结合思想是数学中重要的思想方法．所谓数形结合就是根据数学问题的题设和结论之间的内在联系，既分析其数量关系，又揭示其几何意义使数量关系和几何图形巧妙地结合起来，并充分地利用这种结合，探求解决问题的思路，使问题得以解决的思考方法．

Ⅱ、典型例题剖析

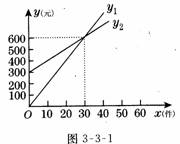
【例1】（2005，嘉峪关，10分）某公司推销一种产品，设x（件）是推销产品的数量，y（元）是推销费，图3－3－1已表示了公司每月付给推销员推销费的两种方案，看图解答下列问题：

  （1）求y₁与y₂的函数解析式；

  （2）解释图中表示的两种方案是如何付推销费的？

  （3）果你是推销员，应如何选择付费方案？

  解：（1）y₁=20x，y₂=10x+300．

      （2）y₁是不推销产品没有推销费，每推销10件产品得推销费200元，y₂是保底工资300元，每推销     10件产品再提成100元．

      （3）若业务能力强，平均每月保证推销多于30件时，就选择y₁的付费方案；否则，选择y₂的付费方案．

点拨：图象在上方的说明它的函数值较大，反之较小，当然，两图象相交时，说明在交点处的函数值是相等的.

【例2】（2005，某农场种植一种蔬菜，销售员张平根据往年的销售情况，对今年这种蔬菜的销售价格进行了预测，预测情况如图3－3－2，图中的抛物线（部分）表示这种蔬菜销售价与月份之间的关系，观察图象，你能得到关于这种蔬菜销售情况的哪些信息？

答题要求：

（1）请提供四条信息；（2）不必求函数的解析．

解：（1）2月份每千克销售价是3．5元；7对月份每千克销售价是0．5元；（3）l月到7月的销售价逐月下降；（4）7月到12月的销售价逐月上升；（5）2月与7月的销售差价是每千克3元；（6）7月份销售价最低，1月份销售价最高；（7）6月与8月、5月与9月、4月与10 月、3月与11 月，2月与12 月的销售价分别相同． 

点拨：可以运用二次函数的性质：增减性、对称性．最大（小）值等，得出多个结论．