开放型试题

开放型试题重在开发思维，促进创新，提高数学素养，所以是近几年中考试题的热点考题。观察、实验、猜想、论证是科学思维方法，是新课标思维能力新添的内容，学习中应重视并应用。

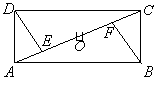例1．（2005年梅州）如图，四边形ABCD是矩形，O是它的中心，E、F是对角线AC上的点。

（1）如果           ，则ΔDEC≌ΔBFA（请你填上能使结论成立的一个条件）；

（2）证明你的结论。

分析：这是一道探索条件、补充条件的开放型试题，解决这类问题的方法是假设结论成立，逐步探索其成立的条件。

解：（1）AE=CF（OE=OF；DE⊥AC；BF⊥AC；DE∥BF等等）

     （2）∵四边形ABCD是矩形，∴AB=CD，AB∥CD，∠DCE=∠BAF

        又∵AE=CF，∴AC－AE=AC－CF，∴AF=CE，∴ΔDEC≌ΔBAF

说明:考查了矩形的性质及三角形全等的判定。

练习一

1. (2005年黑龙江课改）如图, E、F是□ABCD对角线BD上的两点，请你添加一个适当的条件: ___________ ，使四边形AECF是平行四边形.

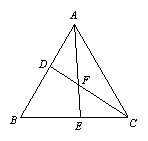
2、（2005年金华）如图，在△ABC中，点D在AB上，点E在BC上，BD＝BE.

（1）请你再添加一个条件，使得△BEA≌△BDC，并给出证明.

你添加的条件是：    .

证明：