|
创新应用题
一、解直角三角形的应用问题
从近几年全国各省市的中考试题来看,直角三角形的解法及其应用,成为中考的热点,它着重考查学生的应用能力与创新能力。
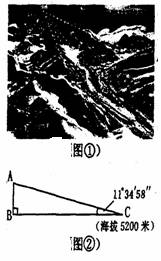 例1.(2005年福建三明市)2005年5月22日,媒体广泛报道了我国“重测珠峰高度”的活动,测量人员从六个不同观察点同时对峰顶进行测量(如图1)。小英同学对此十分关心,从媒体得知一组数据:观察点C的海拔高度为5200米,对珠峰峰顶A点的仰角∠ACB=11°34′58″,AC=18174.16米(如图2),她打算运用已学知识模拟计算。 例1.(2005年福建三明市)2005年5月22日,媒体广泛报道了我国“重测珠峰高度”的活动,测量人员从六个不同观察点同时对峰顶进行测量(如图1)。小英同学对此十分关心,从媒体得知一组数据:观察点C的海拔高度为5200米,对珠峰峰顶A点的仰角∠ACB=11°34′58″,AC=18174.16米(如图2),她打算运用已学知识模拟计算。
⑴现在也请你用此数据算出珠峰的海拔高度(精确到0.01米);
⑵你的计算结果与1975年公布的珠峰海拔高度8848.13米相差多少?珠峰是长高了,不是变矮了呢?
解: ⑴在Rt△ABC中,∵sin∠ACB=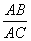
∴AB=AC sin∠ACB=18174.16×sin11°34′58″
≈3649.07
3649.07+5200=8849.07
∴珠峰的海拔高度为8849.07米
⑵8849.07-8848.13=0.94
练习一
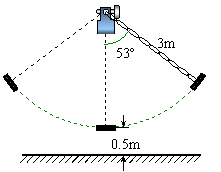 1.(2005年连云港)如图所示,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为 1.(2005年连云港)如图所示,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为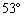 ,则秋千踏板与地面的最大距离约为多少? ,则秋千踏板与地面的最大距离约为多少?
(参考数据: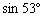 ≈0.8, ≈0.8, ≈0.6) ≈0.6) 2、(2005年河北课改)如图,晚上,小亮在广场 |

