|
一、填空题:(本大题共14小题,每小题5分,共70分)
1.已知集合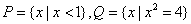 ,则 ,则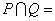 ____________. ____________.
2.在复平面内,复数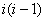 对应的点在第____________象限. 对应的点在第____________象限.
3.甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如下(单位:t / hm2)
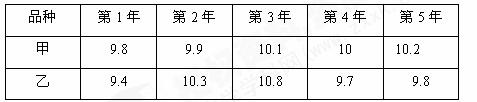
 其中产量比较稳定的小麦品种是 . 其中产量比较稳定的小麦品种是 .
4.函数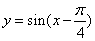 在 在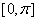 上的单调递增区间是____________. 上的单调递增区间是____________.
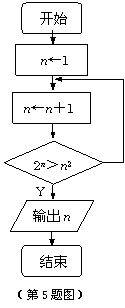
5.执行右边的流程图,最后输出的n的值是 .
6.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出两个小球,则取出的小球上标注的数字之和为5或7的概率是____________.
7.已知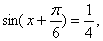 则 则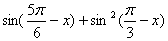 =____________. =____________.
8.已知点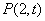 在不等式组 在不等式组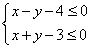 表示的平面区域内,则点 表示的平面区域内,则点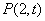 到直线 到直线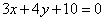 距离的最大值为____________. 距离的最大值为____________.
 9.将一边长为4的正方形纸片按照图中的虚线所示的方法剪开后拼接 9.将一边长为4的正方形纸片按照图中的虚线所示的方法剪开后拼接
为一正四棱锥,则该正四棱锥的体积为 .
10.在数列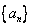 中, 中,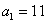 ,且 ,且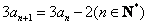 ,则该数列中相邻两项乘积的最小值为__________. ,则该数列中相邻两项乘积的最小值为__________.
11.已知点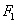 , ,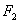 分别是双曲线 分别是双曲线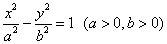 的左、右焦点,过F1且垂直于 的左、右焦点,过F1且垂直于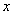 轴的直线与双曲线交于 轴的直线与双曲线交于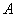 , ,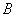 两点,若 两点,若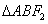 是锐角三角形,则该双曲线离心率的取值范围是____________. 是锐角三角形,则该双曲线离心率的取值范围是____________.
12.设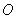 为坐标原点,给定一个定点 为坐标原点,给定一个定点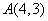 , 而点 , 而点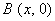 在 在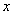 正半轴上移动, 正半轴上移动,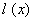 表示 表示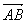 的长,则△ 的长,则△ 中两边长的比值 中两边长的比值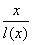 的最大值为 . 的最大值为 .
13.若对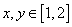 且 且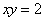 总有不等式 总有不等式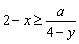 成立,则实数a的取值范围是__________. 成立,则实数a的取值范围是__________.
14.如果对于函数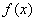 定义域内任意的两个自变量的值 定义域内任意的两个自变量的值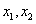 ,当 ,当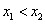 时,都有 时,都有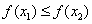 ,且存在两个不相等的自变量值 ,且存在两个不相等的自变量值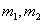 ,使得 ,使得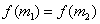 ,就称 ,就称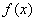 为定义域上的不严格的增函数.已知函数 为定义域上的不严格的增函数.已知函数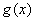 的定义域、值域分别为 的定义域、值域分别为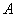 、 、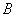 , ,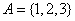 , ,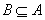 , 且 , 且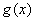 为定义域 为定义域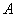 上的不严格的增函数,那么这样的 上的不严格的增函数,那么这样的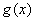 共有____________个. 共有____________个. |

