|
一、填空题(共计4道题,总分70分)
1、已知全集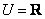 , ,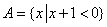 , ,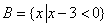 ,那么 ,那么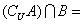 _______. _______.
2、如果复数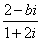 (其中 (其中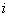 为虚数单位, 为虚数单位,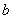 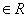 )的实部和虚部互为相反数,那么 )的实部和虚部互为相反数,那么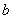
等于______.
3.椭圆的短轴长为2,长轴是短轴的2倍,则椭圆的中心到其准线的距离是
4、已知cos(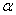 + +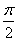 )= )=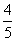 ,且 ,且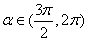 ,则sin ,则sin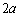 = . = .
5.已知样本方差由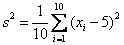 求得,则 求得,则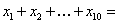 _________________ _________________
6.将一枚骰子抛掷两次,若先后出现的点数分别为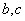 ,则方程 ,则方程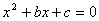 有实 有实
根的概率为 .
7、已知直线m、n,平面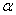 、 、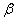 ,且m⊥ ,且m⊥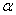 ,n ,n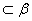 , ,
给出下列命题:
①、若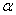 ∥ ∥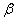 ,则m⊥n; ,则m⊥n;
②、若m⊥n,则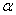 ∥ ∥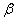 ; ;
③、若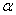 ⊥ ⊥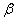 ,则m∥n; ,则m∥n;
④、若m∥n,则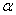 ⊥ ⊥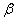 . .
其中正确的命题的序号是
8.如图所示的流程图,输出的结果为
9、函数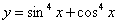 的单调递增区间是___________________ 的单调递增区间是___________________
10、设双曲线C: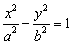 (a>0,b>0)的右焦点为F,O为坐标原点.若以F为圆心,FO为半径的圆与双曲线C的一条渐近线交于点A(不同于O点),则△OAF的面积为 (a>0,b>0)的右焦点为F,O为坐标原点.若以F为圆心,FO为半径的圆与双曲线C的一条渐近线交于点A(不同于O点),则△OAF的面积为
11、直线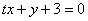 与圆 与圆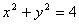 相交于A、B两点,若 相交于A、B两点,若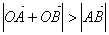 ,则实数t的范围 ,则实数t的范围
12.已知实数a,b,c满足a≤b≤c,且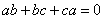 ,abc=1,不等式 ,abc=1,不等式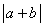 ≥ ≥
恒成立.则实数k的最大值为
13、已知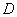 是 是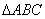 边 边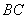 延长线上一点,记 延长线上一点,记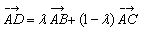 . 若关于 . 若关于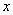 的方程 的方程
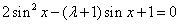 在 在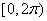 上恰有两解,则实数 上恰有两解,则实数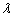 的取值范围是 的取值范围是
14、已知等差数列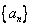 首项为 首项为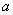 ,公差为 ,公差为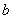 ,等比数列 ,等比数列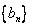 首项为 首项为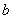 ,公比为 ,公比为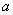 ,其中 ,其中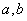 都是大于1的正整数,且 都是大于1的正整数,且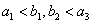 ,对于任意的 ,对于任意的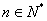 ,总存在 ,总存在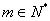 ,使得 ,使得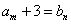 成立,则 成立,则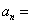
二、解答题(共6道题,总计90分。解答时应写出文字说明、证明过程或演算步骤.)
15、已知向量a=(3sinα,cosα),b=(2sinα, 5sinα-4cosα),α∈(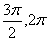 ),且a⊥b. ),且a⊥b.
(1)、求tanα的值;
(2)、求cos(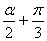 )的值. )的值.
|

