|
21.圆的基本概念性质
 (2010哈尔滨)1.如图,AB是⊙O的弦,半径OA=2,∠AOB=120°,则弦AB的长是( ).B (2010哈尔滨)1.如图,AB是⊙O的弦,半径OA=2,∠AOB=120°,则弦AB的长是( ).B
(A)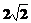 (B) (B)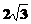 (C) (C)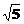 (D) (D)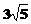
(2010珠海)2.如图,⊙O的半径等于1,弦AB和半径OC互相平分于点M.求扇形OACB的面积(结果保留π)
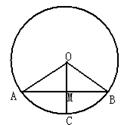 解:∵弦AB和半径OC互相平分 解:∵弦AB和半径OC互相平分
∴OC⊥AB
OM=MC=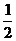 OC= OC=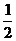 OA OA
在Rt△OAM中,sinA=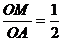
∴∠A=30°
又∵OA=OB ∴∠B=∠A=30° ∴∠AOB=120°
∴S扇形=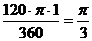
(2010珠海)3.如图,△ABC内接于⊙O,AB=6,AC=4,D是AB边上一点,P是优弧BAC的中点,连结PA、PB、PC、PD.
(1)当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并证明;
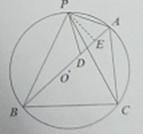 (2)若cos∠PCB= (2)若cos∠PCB= ,求PA的长. ,求PA的长.
解:(1)当BD=AC=4时,△PAD是以AD为底边的等腰三角形
∵P是优弧BAC的中点 ∴弧PB=弧PC
∴PB=PC
∵BD=AC=4 ∠PBD=∠PCA
∴△PBD≌△PCA
∴PA=PD 即△PAD是以AD为底边的等腰三角形
(2)由(1)可知,当BD=4时,PD=PA,AD=AB-BD=6-4=2
过点P作PE⊥AD于E,则AE=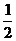 AD=1 AD=1
∵∠PCB=∠PAD
∴cos∠PAD=cos∠PCB= |

