平抛运动“四问题”
平抛运动可以看作水平方向的匀速直线运动和自由落体运动的合运动.由于竖直分运动为自由落体运动,则匀变速直线运动的解题方法和技巧都可以用到平抛运动中来.
一 平抛运动中实验数据问题
例1 (2009扬州大学附中一摸)在“研究平抛运动”的实验中,为了得到平抛运动的轨迹,可以采用描迹法,也可以采用拍摄闪光照片的方法.
(1)为了描绘出小球平抛运动的轨迹,实验时按图1(a)安装好器材,需注意斜槽末端 ,并让小球多次从 位置上滚下.
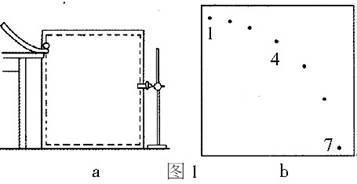
(2)如图1(b)所示,为一平抛物体运动的闪光照片示意图,照片与实际大小相比缩小到1/10.对照片中小球的位置进行测量,可得1与4闪光点竖直距离为1.5cm,4与7闪光点竖直距离为2.5cm,各闪光点之间水平距离均为0.5cm.则小球抛出时的速度大小为 m/s;抛出点距闪光点1的实际水平距离为 cm,实际竖直距离为 cm.(不计空气阻力,g取10m/s2)
解析: (1)水平,保证小球做平抛运动,从同一位置滚下,使初速度相同.
(2)在竖直方向,由s74-s41=gT2得T=0.1s.
又由 得v0=1.5m/s.由 得v0=1.5m/s.由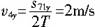 ,得v1y=1m/s,再由v21y=2gh1得h1=5cm,又由v1y=gT1,得T1=0.1s,x1=15cm ,得v1y=1m/s,再由v21y=2gh1得h1=5cm,又由v1y=gT1,得T1=0.1s,x1=15cm
答案:1.5 15 5
二 平抛运动中对称性问题
例2 如图2所示在一房间内靠近右墙的A点处,沿水平方向抛出一个小球与左墙B点碰撞,碰撞前后竖直速度不变,水平速度等大反向,最后落在C处,已知A点与C点的高度差为H,则B点与C点的高度差为多少?
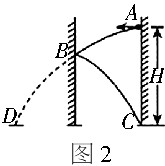
解析:小球在B点和墙壁碰撞时竖直速度不变,水平速度等大反向,由于水平位移相同,则AB段和BC段对应的时间相同.由对称性可知,BC段可以和BD段等效,则从A→B→C的运动可以等效为从A→B→D的运动.由自由落体运动的特点可知,AB段和BC段竖直位移之比为1:3,因此BC段的竖直位移为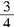 H. H.
三 平抛运动中的临界问题
例3 如图3所示,一高度为h=0.2m的水平面在B点处与一倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在平面上向右运动.求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2).
某同学对此题的解法为:小球沿斜面运动,则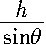 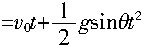 由此可求得落地的时间t. 由此可求得落地的时间t.
问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果.

解析:由于小球在水平面上运动,离开A点时小球将做平抛运动,而不会沿斜面下滑,在运动到地面之前是否经历斜面,则要看具体条件.
正确做法为:落地点与B点的水平距离
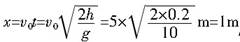
斜面底宽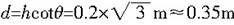
因为x>d,所以小球离开B点后不会落到斜面,因此落地时间即为平抛运动时间.
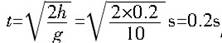
四 平抛运动的拓展—类平抛运动
例4 如图4所示,光滑斜面长为a,宽为b,倾角为θ,一物块沿斜面左上方顶点P水平射入,而从右下方顶点Q离开斜面,求入射初速度.
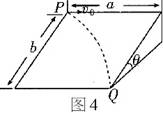
解析: 物块在垂直于斜面方向没有运动,物块沿斜面方向上的曲线运动可分解为水平方向上初速度为v0的匀速直线运动和沿斜面向下初速度为零的匀加速运动.
在沿斜面方向上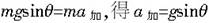 ……① ……①
水平方向上的位移x=a=v0t………………………②
沿斜面向下的位移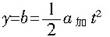 ………………③ ………………③
由①②③得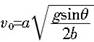
|

