|
万有引力定律的应用 学案
1.关于万有引力和重力的关系
地面上物体所受万有引力F可以分解为物体所受的重力mg和随地球自转而做圆周运动的向心力F’。其中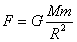 
① 当物体在赤道上时,F、mg、F’三力同向,此时满足F’+mg=F
② 当物体在两极点时,F’=0 ,F=mg=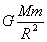
③ 当物体在地球的其他位置时,三力方向不同。
例1 地球赤道上的物体由于地球自转产生的向心加速度a=3.37×10-2 m/s2,赤道上重力加速度 g取10m/s2试问:(1)质量为m kg的物体在赤道上所受的引力为多少?(2)要使在赤道上的物体由于地球的自转而完全失重,地球自转的角速度应加快到实际角速度的多少倍? g取10m/s2试问:(1)质量为m kg的物体在赤道上所受的引力为多少?(2)要使在赤道上的物体由于地球的自转而完全失重,地球自转的角速度应加快到实际角速度的多少倍?
解析:(1)物体所受地球的万有引力产生了两个效果:一是使物体竖直向下运动的重力,一是提供物体随地球自转所需的向心力,并且在赤道上这三个力的方向都相同,有F引=mg+F向=m(g+a)=m(9.77+3.37×10-2)=9.804m(N)
(2)设地球自转角速度为ω,半径为R,则有a=ωR,欲使物体完全失重,即万有力完全提供了物体随地球自转所需的向心力,即mω’R=F引=9.804m,解以上两式得ω’=17.1ω.
2.关于天体质量或密度的计算问题
解法一:利用天体表面的重力加速度g,由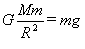 得M=gR2/G,只需知道g和天体半径R即可;密度 得M=gR2/G,只需知道g和天体半径R即可;密度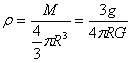
解法二:利用“卫星 ”的周期T和半径r,由 ”的周期T和半径r,由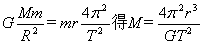 , ,
密度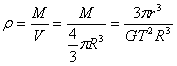 (R为天体的半径),当卫星沿天体表面附近绕天体运动时,r=R,则 (R为天体的半径),当卫星沿天体表面附近绕天体运动时,r=R,则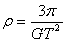 。 。
例2 已知引力常量G=6.67×10-11N·m2/kg2,重力加速度g=9.8m/s2,地球半径R=6.4×104m,可求得地球的质量为多少?(结果保留一位有效数字)
解析:在地球表面质量为m的物体所受的重力等于地球对物体的引力,有
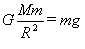 ,得 ,得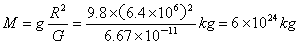
例3 一飞船在某行星表面附近沿圆轨道绕该行星飞行,认为行星是密度均匀的球体,要确定该行星的密度,只需要测量
|

