|
图1-1-2为一空间探测器的示意图,P1、P2、P3、P4是四个喷气发动机,P1、P3的连线与空间一固定坐标系的x轴平行,P2、P4的连线与y轴平行.每台发动机喷气时,都能向探测器提供推力,但不会使探测器转动.开始时,探测器相对于坐标系以恒定的速率v0沿正x方向平动.先开动P1,使P1在极短的时间内一次性喷出质量为m的气体,气体喷出时相对于坐标系的速度大小为v.然后开动P2,使P2在极短的时间内一次性喷出质量为m的气体,气体喷出时相对坐标系的速度大小为v.此时探测器的速度大小为2v0,且方向沿正y方向.假设探测器的总质量为M(包括气体的质量),求每次喷出气体的质量m与探测器总质量M的比值和每次喷出气体的速度v与v0的比值.
解析:探测器第一次喷出气体时,沿x方向动量守恒,且探测器速度变为零.
即Mv0=mv①
第二次喷出气体时,沿y方向动量守恒:0=(M-2m)·2v0-mv②
解①②得:=,=.
答案: 4
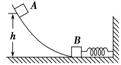
图1-1-3
2. 如图1-1-3所示,一轻质弹簧的一端固定在墙上,另一端系有一静止在光滑水平面上的物体B.有一质量与B相同的物体A从高h处由静止开始沿光滑的曲面滑下,与B发生碰撞一起将弹簧压缩后,A与B重新分开,A又沿曲面上升,求能达到的最大高度 解析:A从h高处滑下与B碰前的速度v0=,与B发生完全非弹性碰撞,有2mv=mv0,得v= ,A和B一起压缩弹簧,机械能守恒,回到碰撞点时的速度仍然为v,分离后A以速度v滑上光滑斜面,由mgh′=mv2, |

