1．如图8－3－8所示，ABC为与匀强磁场垂直的边长为a的等边三角形，磁场垂直纸面向外，比荷为e/m的电子以速度v₀从A点沿AB方向射入，现欲使电子能经过BC边，则磁感应强度B的取值应为(　　)

       A．B>       B．B<       C．B<  D．B>

       解析：当电子从C点离开时，电子做圆周运动对应的轨道半径最小，有R>＝，而R＝，所以B<，C项正确．

       答案：C

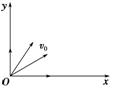
图8－3－9

2．在xOy平面内有许多电子(质量为m，电荷量为e)从坐标原点O不断以相同大小的速度v₀沿不同的方向射入第一象限，如图8－3－9所示．现加上一个垂直于xOy平面向里的磁感应强度为B的匀强磁场，要求这些电子穿过该磁场后都能平行于x轴向x轴正方向运动，试求出符合条件的磁场的最小面积．

       解析：所有电子在所求的匀强磁场中均做匀速圆周运动，由ev₀B＝m，得半径为R＝.

       设与x轴正向成α角入射的电子从坐标为(x，y)的P点射出磁场，

       则有x²＋(R－y)²＝R²①