|
快乐闯关:
勾股定理与实数(原创精品)
考点1:勾股定理及其逆定理
例1.(2010辽宁丹东) 图①是一个边长为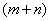 的正方形,小颖将 的正方形,小颖将
图①中的阴影部分拼成图②的形状,由图①和图②
能验证的式子是( )
A.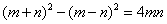
B.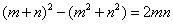
C.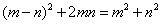
D.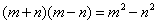
解析:本题综合考查正方形的性质、全等三角形的判定与性质、勾股定理及三角形的面积公式。由图①,根据正方形的性质、全等三角形的判定可得阴影部分的4个直角三角形全等,且易得中间的空白部分是正方形,根据勾股定理得其边长为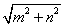 ,所以阴影部分的面积= ,所以阴影部分的面积=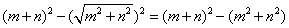 ;由图②,阴影部分的面积=四边形的面积=4个直角三角形的面积= ;由图②,阴影部分的面积=四边形的面积=4个直角三角形的面积= 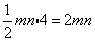 ,所以 ,所以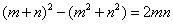 ,B正确。 ,B正确。
答案:B。
例2(2010杭州月考)如图,在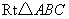 中, 中,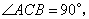 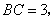 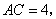 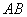 的垂直平分线 的垂直平分线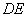 交 交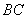 的延长线于点 的延长线于点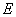  ,则 ,则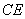 的长为( ) 的长为( )
(A)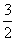 (B) (B) 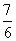 (C) (C)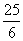 (D)2 (D)2
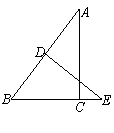
解析:本题综合考查勾股定理、直角三角形相似的判定与性质。观察图形,要求CE,只需求得BE的长,再由BE-BC即可,将问题转化为求BE的长。 中, 中, 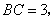 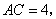 根据勾股定理得AB=5。由DE垂直平分AB得 根据勾股定理得AB=5。由DE垂直平分AB得
BD=2.5,∠BDE=90°。又因为∠B是公共角,所以△ABC∽△EBD,所以AB:BE=BC:BD,即5:BE=3:2.5,解得BE=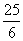 ,所以CE=BE-3= ,所以CE=BE-3=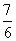 ,B正确。 ,B正确。
答案:B。
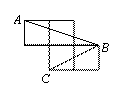 例3(2010四川眉山)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则 例3(2010四川眉山)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则
∠ABC的度数为( )
A.90° B.60° C.45° D.30° |

