|
第一部分 集合与常用逻辑用语
一、知识梳理
(一)基础知识:见步步高文科P106;理科P118。
(二)要点梳理:
1.在集合运算中一定要分清代表元素的含义,如分清是数集还是点集、是x还是y等.
[例]已知集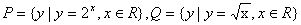 ,求 ,求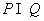 . (答案: . (答案: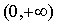 ) )
2.空集的存在性(空集是任何集合的子集,空集是任何非空集合的真子集).见步步高要点回扣:2
3、对于含有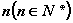 个元素的有限集合M,其子集,真子集,非空子集,非空真子集的个数依次为2n,2n-1,2n-1,2n-2。 个元素的有限集合M,其子集,真子集,非空子集,非空真子集的个数依次为2n,2n-1,2n-1,2n-2。
另外:①进行集合的交、并、补运算时,不要忘记了借助数轴和文氏图进行求解,注意端点值。
②你会用补集的思想解决有关问题吗?
③求不等式(方程)的解集,或求定义域(值域)时,你按要求写成集合的形式了吗?
4.充要条件的判定可利用集合包含思想判定:若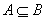 ,则 ,则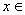 A是 A是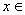 B的充分条件;若 B的充分条件;若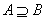 ,则 ,则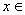 A是 A是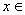 B的必要条件;若 B的必要条件;若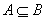 且 且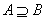 即 即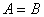 ,则 ,则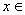 A是 A是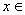 B的充要条件. B的充要条件.
5.充要条件的问题要十分细心地去辨析:“哪个命题”是“哪个命题”的充分(必要)条件;注意区分:“甲是乙的充分条件(甲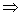 乙)”与“甲的充分条件是乙(乙 乙)”与“甲的充分条件是乙(乙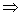 甲)”,是两种不同形式的问题. 甲)”,是两种不同形式的问题.
6.掌握命题的四种不同表达形式,会进行命题之间的转化,会正确找出命题的条件与结论.能根据条件与结论判断出命题的真假. 有时利用“原命题”与“逆否命题”等价,“逆命题”与“否命题”等价转换去判定也很方便.
二.易错、易混、易忘知识点提醒:
例1.设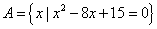 , ,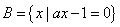 ,若 ,若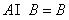 ,求实数a组成的集合的子集有多少个? ,求实数a组成的集合的子集有多少个?
解析:集合A化简得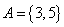 ,由 ,由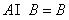 知 知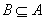 故(Ⅰ)当 故(Ⅰ)当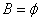 时,即方程 时,即方程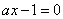 无解,此时a=0符合已知条件(Ⅱ)当 无解,此时a=0符合已知条件(Ⅱ)当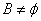 时,即方程 时,即方程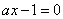 的解为3或5,代入得 的解为3或5,代入得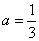 或 或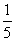 。综上满足条件的a组成的集合为 。综上满足条件的a组成的集合为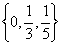 ,故其子集共有 ,故其子集共有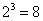 个。 个。
|

