|
教学目标:
经历探索平方差公式的过程.会推导平方差公式,并能运用公式进行简单的运算,培养学生观察、归纳、概括的能力.
教学重点:平方差公式的推导和应用.理解平方差公式的结构特征,灵活应用平方差公式.
教学过程设计:
|
设计意图 |
(一) 学生动手,得到公式
1. 计算下列多项式的积.
(1)(x+1)(x-1) (2)(m+2)(m-2)
(3)(2x+1)(2x-1) (4)(x+5y)(x-5y)
2.提出问题:
观察上述算式,你发现什么规律?运算出结果后,你又发现什么规律?
3.特点:
等号的一边:两个数的和与差的积,等号的另一边:是这两个数的平方差
4.再试一试:
【学生自己出相似的题目加以验证】
5.得到结论
(a+b)(a-b)=a2-ab+ab-b2=a2-b2.
即 (a+b)(a-b)=a2-b2 【1】
(二) 熟悉公式
1.下列哪些多项式相乘可以用平方差公式?
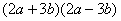 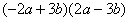
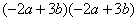 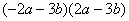
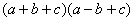 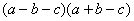
1. 认清公式:在等号左边的两个括号内分别没有符号变化的集团是a,变号的是b
(三) 运用公式
1. 直接运用
例:(1)(3x+2)(3x-2)(2)(b+2a)(2a-b)(3)(-x+2y)(-x-2y)
2. 简便计算
例:(1)102×98【3】 (2)(y+2)(y-2)-(y-1)(y+5)
3. 练习: P153 练习1,2
 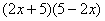
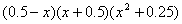 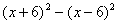
100.5×99.5 99×101×10001 | |

