一、选择题

1．(2009年河池模拟)在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28，……这些数叫做三角形数，因为这些数对应的点可以排成一个正三角形(如下图所示)则第n个三角形数为(　　)

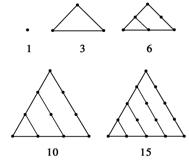
A．n　　　　　　　　　　 B.n(n＋1)

C．n²－1                 D.n(n－1)

2. 凸n边形有f(n)条对角线，则凸n＋1边形有f(n＋1)条对角线数为(　　)

A．f(n)＋n－1             B．f(n)＋n

C．f(n)＋n＋1             D．f(n)＋n－2

3．设f₀(x)＝cos x，f₁(x)＝f₀′(x)，f₂(x)＝f₁′(x)，…，f_n＋1(x)＝f_n′(x)，n∈N^*，则f₂₀₁₁(x)＝(　　)

A．－sin x                 B．－cos x

C．sin x                    D．cos x

4．(2010年福建三明期末)给出下面类比推理命题(其中R为实数集，C为复数集)：

①“若a，b∈R，则a－b＝0⇒a＝b”类比推出“若a，b∈C，则a－b＝0⇒a＝b”；

②“若a，b，c，d∈R，则复数a＋bi＝c＋di⇒a＝c，b＝d”类比推出“若a，b，c，d∈C，则复数a＋bi＝c＋di⇒a＝c，b＝d”；

③“若a，b∈R，则a－b>0⇒a>b” 类比推出“若a，b∈C，则a－b>0⇒a>b”；

④“若a，b∈R，则a·b＝0⇒a＝0或b＝0”．类比推出“若a，b∈C，则a·b＝0⇒a＝0或b＝0”．

其中类比结论正确的个数是(　　)

A．0                       B．1

C．2                        D．3