5.5 角平分线的性质

目的要求：

1. 学会用尺规作图画角平分线.

2. 认识角平分线的性质.

3. 理解在三角形中三条角平分线的交点与三边的关系.

4. 进行角平分线的有关应用.

重点：

角平分线的性质.

准备：

作图工具、小黑板、幻灯

过程：

一、复习.（幻灯）

1. 三角形的内角和与外角和.多边形的内角和与外角和.

2. 三角形按两类分，分为哪两类？按三类分，又是怎样分的？

3. 三角形三 边的关系.

4. 直角三角形中两锐角的关系.

二、角平分线画法.

1. 角平分线的定义.

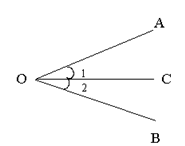角平分线是从一个引出的一条把角分为相等的两个角的射线.

如图：∵在∠AOB中，∠1＝∠2

      ∴OC为∠AOB的角平分线

2. 角平分线的画法.

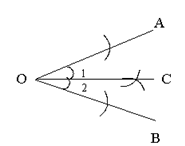对折法：用轴对称的原理，把一个角沿某一直线对折，并使角的两边能够重合，则顶点为角的顶点且过折痕的射线即为角平分线.

局限性：不方便！在黑板上画一个角的平分线是不可能对折的.

尺规法：如图，作法略.

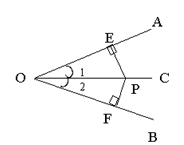
三、角平分线的性质.

1.       通过测量的形式探讨PE＝PF.

2. 通过轴对称的原理探讨PE＝PF.

（注意强调：点到直线的距离是垂线.）

性质：角平分线上的点到角两边的距离相等.

反之：到角两边距离相等的点在角平分线上.

四、应用.（小黑板）

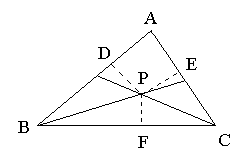1. 探讨△ABC的三条角平分线的交点与三边的距离关系.

得结：三角平分线的交点到三边的距离相等.

用图形说明：

在△ABC中，BP平分∠ABC，

PC平分∠ACB,

∴PE＝PF＝PD

即：可以以交点为圆心，交点到某一边距离的长为半径在三角形内作一个最大的圆.

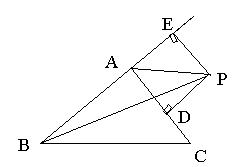2. 如图：△ABC的外角平分线AP上有一点P,且PE⊥BE，PD⊥AC，E、D分别为垂足，则EB＋PD＝PB吗？说明理由.