|
解决空间图形问题的四大“法宝”
立体几何试题是高考必须拿下的“奶酪”!其多以平行、相交、垂直、角、距离、面积和体积问题为载体,以点、线、面的各种位置关系以及球体为对象命题,重在考查学生是否具备扎实的基础知识和基本技能,破解的“法宝”则是推理、想象、转化和计算能力.
一、推理能力
例1 对于任意直线l与平面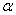 ,在平面 ,在平面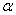 内必有直线m,使m与l( ). 内必有直线m,使m与l( ).
(A)平行 (B)相交
(C)垂直 (D)互为异面直线
解析:抓住题中的关键词“任意”与“必有”,那么l可以在平面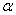 外,也可以在平面 外,也可以在平面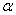 内;当l在平面 内;当l在平面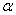 外时,还有与平面 外时,还有与平面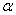 相交与平行两种可能,不管在何种情况下,平面 相交与平行两种可能,不管在何种情况下,平面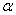 内必有直线m⊥l,故选(C). 内必有直线m⊥l,故选(C).
点评:突出考查的是空间想象能力和推理能力,应该为这道小而巧的题目叫好!
例2 若一条直线与正四棱柱的各个面所成的角都为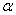 ,则 ,则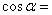 _______. _______.
解析:最特殊的正四棱柱为正方体,它的对角线与其各个面所成
的角都相等,连图形都不用画,就可得这个角的余弦值为.在一般
情况下,该结论是否仍然成立?考虑图1,不管将正方体纵向延伸
或压缩,原来正方体的对角线PQ仍然满足题设条件.这个结果是多
么地激动和鼓舞人心!
点评:特殊化是解选择、填空题的一种重要方法,从特殊到一般的推理能力是必备的素质. |

