|
q的
[ ]
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
分析 利用韦达定理转换.
解 ∵x1,x2是方程x2+5x-6=0的两根,
∴x1,x2的值分别为1,-6,
∴x1+x2=1-6=-5.[来源:学#科#网]
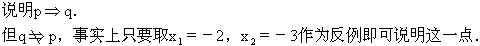
因此选A.
说明:判断命题为假命题可以通过举反例.
例2 p是q的充要条件的是
[ ]
A.p:3x+2>5,q:-2x-3>-5
B.p:a> 2,b<2,q:a>b 2,b<2,q:a>b
C.p:四边形的两条对角线互相垂直平分,q:四边形是正方形
D.p:a≠0,q:关于x的方 程ax=1有惟一解 程ax=1有惟一解
分析 逐个验证命题是否等价.[来源:学,科,网Z,X,X,K]
解 对A.p:x>1,q:x<1,所以,p是q的既不充分也不必要条件;
对B.p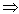 q但q q但q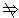 p,p是q的充分非必要条件; p,p是q的充分非必要条件;
对C.p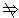 q且q q且q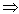 p,p是q的必要非充分条件; p,p是q的必要非充分条件;
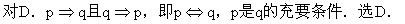
说明:当a=0时,ax=0有无数个解.
例3 若A是B成立的充分条件,D是C成立的必要条件,C是B成立的充要条件,则D是A成立的
[ ]
A.充分条件 B.必要条件
C.充要条件 D.既不充分也不必要条件
分析 通过B、C作为桥梁联系A、D.
解  ∵A是B的充分条件,∴A ∵A是B的充分条件,∴A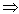 B① B①
∵D是C成立的必要条件,∴C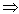 D② D②
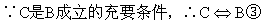
由①③得A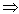 C④ C④
由②④得A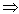 D. D.
∴D是A成立的必要条件.选B.
说明:要注意利用推出符号的传递性.
例4 设命题甲为:0<x<5,命题乙为|x-2|<3,那么甲是乙的
[ ]
A.充分不必要条件 B.必要不充分条件
C.充要条件 D. 既不充分也不必要条件 既不充分也不必要条件
分析 先解不等式再判定. |

