|
知抛物线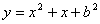 经过点 经过点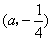 和 和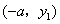 ,则 ,则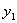 的值是 . 的值是 .
11.已知二次函数y=ax2+bx+c的图象与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3),则二次函数的解析式是 .
12.若函数y=3x2与直线y=kx+3的交点为(2,b),则k=__,b=__.
13.函数y=9-4x2,当x=_________时有最大值________.
14.两数和为10,则它们的乘积最大是_______,此时两数分别为________.
三、解答题(共52分)
15.求下列函数的图像的对称轴、顶点坐标及与x轴的交点坐标.
(1)y=4x2+24x+35; (2)y=-3x2+6x+2; (3)y=x2-x+3; (4)y=2x2+12x+18.
16.已知抛物线C1的解析式是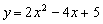 ,抛物线C2与抛物线C1关于x轴对称,求抛物线C2的解析式. ,抛物线C2与抛物线C1关于x轴对称,求抛物线C2的解析式.
17.填表并解答下列问题:
|
x |
… |
-1 |
0 |
1 |
2 |
… |
|
y1=2x+3 |
… |
… |
|
|
|
|
|
y2=x2 |
… |
… |
|
|
|
|
(1)在同一坐标系中画出两个函数的图像.
(2)当x从1开始增大时,预测哪一个函数的值先到达16.
(3)请你编出一个二次项系数是1的二次函数,使得当x=4时,函数值为16.编出的函数解析式是什么?
18.已知抛物线y=x2-2x-8.
(1)试说明该抛物线与x轴一定有两个交点.
(2)若该抛物线与x轴的两个交点分别为A、B(A在B的左边),且它的顶点为P,求△ABP的面积.
19.已知:如图3,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
(1)用含y的代数式表示AE.
(2)求y与x之间的函数关系式,并求出x的取值范围.
 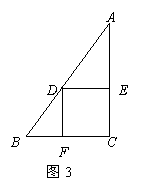 (3)设四边形DECF的面积为S,求出S的最大值. (3)设四边形DECF的面积为S,求出S的最大值.
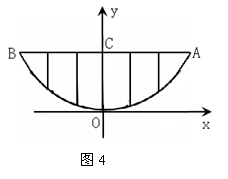
20.某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图4所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
(1) 以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2的解析式;
(2)计算一段栅栏所需立柱的总长度(精确到0.1米).
|

