3.1.1平行四边形的性质和中心对称图形（2）

教学目标

1 使学生进一步掌握平行四边形的性质-----平行四边形的对角线相等.

2 了解中线对称图形的概念，知道平行四边形是中心对称图形.

教学重点、难点：

重点：平行四边形与对角线有关的性质以及理解中心对称图形的概念.

难点：平行四边形性的运用以及中心对称图形的概念的理解

教学过程

一创设情景，导入新课

1 复习：

（1）什么叫平行四边形？

有两组对边分别平行的四边形叫平行四边形.

（2）怎样理解这个概念呢？

从概念知道：一方面，如果一个四边形是平行四边形那么这个四边形的对边一定平行.另一方面，要判断一个四边形是平行四边形，只要判定这个四边形的两组对边分别平行就可以了.

（3） 平行四边形有什么性质？

平行四边形的对边相等， 对角相等.

（4）这个性质是利用什么道理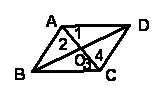得到的？

利用全等三角形的性质得到的

A ∵四边形ABCD是平行四边形，∴AD∥BC,AB∥DC

∴∠1=∠3, ∠2=∠4,

又∵AC=CA, ∴△ABC≌△CDA

∴AB=CD,AD=BC

B ∵△ABC≌△CDA，∴∠B=∠D,

∵∠1=∠3, ∠2=∠4, ∴∠1+∠2=∠3+∠4,即：∠BAD=∠BCD

平行四边形还有什么性质呢?这节课我们继续学习-----3.1.1平行四边形的性质和中心对称(2)

二合作交流,探究新知

1 平行四边形对角线具有的性质

探究活动:

（1）量一量P 72 图3-10中的线段OA、OC、OB、OD的长，并比较OA、OC、OB、OD的大小,由此你能得到什么结论？

估计学生会想到：（1）平行四边形的对角线互相平分,（3）平行四边形的对角线的交点是每条对角线的中点.(3)平行四边的对角线不一定相等.

（2）你知道平行四边形的对角线为什么互相平分吗？

∵四边形ABCD是平行四边形，∴AD∥BC,AB∥DC

∴∠1=∠3, ∠2=∠4,

又∵AC=CA, ∴△ABC≌△CDA

∴OA=OC,OB=OD

(3)请你用语言把平行四边形的这条性质叙说出来.

平行四边形的对角线互相平分.

即：如果四边形ABCD是平四边形，那么OA=OC，OB=OD.

2 中心对称图形的概念

做一做：