|
f(x)=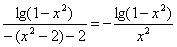 . .
∵f(-x)=-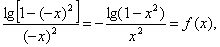 ∴f(x)为偶函数. ∴f(x)为偶函数.
(3)x<-1时,f(x)=x+2,-x>1,
∴f(-x)=-(-x)+2=x+2=f(x).
x>1时,f(x)=-x+2,
-x<-1,f(-x)=x+2=f(x).
-1≤x≤1时,f(x)=0,-1≤-x≤1,
f(-x)=0=f(x).
∴对定义域内的每个x都有f(-x)=f(x).
因此f(x)是偶函数.
2.已知函数y=f(x)的定义域为R,且对任意a,b∈R,都有f(a+b)=f(a)+f(b),且当x>0时,f(x)<0恒成立,f(3)=-3.
(1)证明:函数y=f(x)是R上的减函数;
(2)证明:函数y=f(x)是奇函数;
(3)试求函数y=f(x)在[m,n](m,n∈Z)上的值域.
(1)证明 设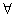 x1,x2∈R,且x1<x2,f(x2)=f[x1+(x2-x1)]=f(x1)+f(x2-x1). x1,x2∈R,且x1<x2,f(x2)=f[x1+(x2-x1)]=f(x1)+f(x2-x1).
∵x2-x1>0,∴f(x2-x1)<0.∴f(x2)=f(x1)+f(x2-x1)<f(x1).
故f(x)是R上的减函数.
(2)证明 ∵f(a+b)=f(a)+f(b)恒成立,∴可令a=-b=x,则有f(x)+f(-x)=f(0),
又令a=b=0,则有f(0)=f(0)+f(0),∴f(0)=0.从而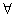 x∈R,f(x)+f(-x)=0, x∈R,f(x)+f(-x)=0,
∴f(-x)=-f(x).故y=f(x)是奇函数.
(3)解 由于y=f(x)是R上的单调递减函数,
∴y=f(x)在[m,n]上也是减函数,故f(x)在[m,n]上的最大值f(x)max=f(m),最小值f(x)min=f(n).
由于f(n)=f(1+(n-1))=f(1)+f(n-1)=…=nf(1),同理f(m)=mf(1).
又f(3)=3f(1)=-3,∴f(1)=-1,∴f(m)=-m,f(n)=-n.
∴函数y=f(x)在[m,n]上的值域为[-n,-m].
3.设f(x)是定义在R上的偶函数,其图象关于直线x=1对称,对任意x1、x2∈[0,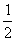 ]都有f(x1+x2) ]都有f(x1+x2)
=f(x1)·f(x2),且f(1)=a>0.
(1)求f(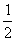 )及f( )及f(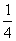 ) )
(2)证明:f(x)是周期函数;
(3)记an=f(2n+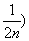 ,求an. ,求an.
(1)解 ∵对x1、x2∈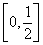 , ,
都有f(x1+x2)=f(x1)·f(x2),
∴f(x)=f(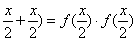 ≥0,x∈[0,1]. ≥0,x∈[0,1].
∴f(1)=f(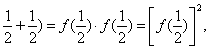
f(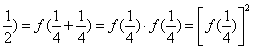 . .
∵f(1)=a>0, ∴f( |

