33.4几 何 概 率

教学目标

知识与技能：理解几何概率的意义，会求简单事件的几何概率，会应用几何概率解决有关实际问题．

数学思考：经历猜想、探索等数学活动过程，积累数学活动经验，发展合情推理能力．

解决问题：能从数学的角度理解问题，能用几何概率等知识解决问题，发展应用意识．

情感态度与价值观：通过解决现实生活的问题，培养学生乐于应用数学的态度，有助于形成勤于探索的精神．

重点、难点

重点：理解几何概率的意义，能借助几何图形的度量求简单事件的概率．

难点：将实际问题转化为数学问题，建立几何概率模型．

透彻理解几何概率的意义．

教学过程设计

一、情境引入      

借助多媒体演示转盘游戏．提出问题“转动圆盘，停下时，指针停留的位置有多少种？指向哪种颜色区域的可能性大？这个问题的概率和以往研究的概率类型一样吗？它有什么特点？”

通过此情境的创设使学生感受到几何概型的特点，及学习它的必要性．激发学生要学习几何概率的欲望．

二、猜想探究、形成概念   

引例1：如图，转动圆盘，等停下时指针指向红色区域的概率是多大？

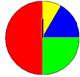
引例2：在数轴上0到60之间任取一点，那么该点落在40到60之间的概率是多大？

借助多媒体动画演示，进一步让学生感受几何概型的特点（事件的等可能结果不可数），对事件的概率得出猜想，并借助教具实验估算概率．

通过对以上两个引例共同特点的讨论，形成几何概率的概念．