|
第三十章反比例函数导学
反比例函数问题大致有求函数的表达式,研究函数的图像与性质,解相关综合题等.本章内容虽说不多,但对知识的理解要求较高,其中还蕴含着丰富的数学思想和方法,请同学们务必认真体会,下面对整章内容作一梳理,希望对同学们有所帮助.
一、知识梳理
1.理解反比例函数的概念应注意两点:(1)自变量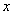 的次数是 的次数是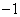 ,(2)比例系数 ,(2)比例系数 . .
2.反比例函数自变量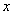 的取值范围是 的取值范围是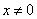 ,因此在画函数图像时,不要把两个分支连结起来,“两个分支都无限接近但永远不能到达 ,因此在画函数图像时,不要把两个分支连结起来,“两个分支都无限接近但永远不能到达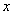 轴和 轴和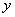 轴”这是由自变量的取值范围所决定的. 轴”这是由自变量的取值范围所决定的.
3.反比例函数的性质可借助下述方法来帮助理解.具有下列条件之一,可推出其他两点:(1)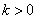 ,(2)图像的两个分支分别在第一、三象限,(3)在每个象限内, ,(2)图像的两个分支分别在第一、三象限,(3)在每个象限内,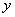 随 随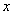 的增大而减小(对于 的增大而减小(对于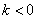 可作同样的分解帮助理解). 可作同样的分解帮助理解).
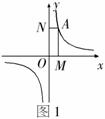 注:(1)反比例函数的增、减一定要强调“在每个象限内”这一前提,因为 注:(1)反比例函数的增、减一定要强调“在每个象限内”这一前提,因为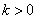 时函数图像的两个分支分别在第一、三象限,若点 时函数图像的两个分支分别在第一、三象限,若点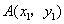 在第一象限的图像上,点 在第一象限的图像上,点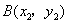 在第三象限的图像上,虽然 在第三象限的图像上,虽然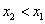 ,但显然 ,但显然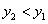 ,即随着 ,即随着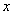 的增大, 的增大,
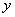 并没有随之变小. 并没有随之变小.
(2)该性质记忆时应“数形结合”,切忌死记硬背.
4.双曲线既是中心对称图形,又是轴对称图形.
5.一个重要结论. 设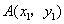 是反比例函数 是反比例函数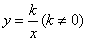 图像上的任意一点,过点 图像上的任意一点,过点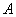 分别作 分别作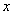 轴、 轴、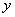 轴的垂线 轴的垂线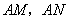 ,则所得矩形 ,则所得矩形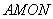 的面积等于 的面积等于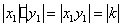 ;同理过点 ;同理过点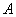 向某一坐标轴作垂线,垂足与 向某一坐标轴作垂线,垂足与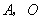 |

