|
2.2 一元二次方程的解法(1)同步练习
解题示范
例 用配方法解下列一元二次方程:
(1)x2+12x=9 964; (2)9x2-12x=1.
审题 本题要求用配方法解一元二次方程,因此方程的左边应先化成(ax+b)2的形式.
方案 对于第(1)小题,配方较为容易,只需两边都加上36即可.对于第(2)小题,联想公式(a+b)2=a2+2ab+b2,应在方程两边都加上4,才能把左边的式子化成(ax+b)的形式.
实施 (1)x2+12x=9 964.
两边都加上36,得x2+12x+36=9 964+36.
即(x+6)2=10 000.
∴ x+6=100,或x+6=-100.
解得x1=94,x2=-106.
(2)9x2-12x=1.
两边都加上4,得9x2-12x+4=1+4,即(3x-2)2=5.
∴ 3x-2=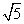 ,或3x-2=- ,或3x-2=-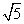 . .
解得 x1=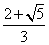 ,x2= ,x2=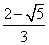 . .
反思 对二次项系数为1的一元二次方程进行配方,应在方程两边都加上一次项系数一半的平方.
课时训练
1.填上适当的数,使下列等式成立:
(1)x2+2x+________=(x+______)2;(2)x2-6x+________=(x-______)2;
(3)t2-10t+________=(t-_______)2;(4)y2+_____y+121=(y+_______)2.
2.方程(x+1)2=9的解是_________.
3.在横线上填上适当的数或式,使下列等式成立:
(1)x2+px+________=(x+_______)2;(2)x2+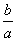 x+_________=(x+_______)2. x+_________=(x+_______)2.
4.解方程:
(1)x2=121; (2)(x-3)2=16.
|

