5．2 平行四边形同步练习

解题示范

例  在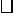ABCD中，DE⊥AB于点E，DF⊥BC于点F，且∠ADE+∠CDF=60°，求∠EDF的度数．

    审题  在ABCD中，已知条件有∠AED=∠CFD=90°，∠ADE+∠CDF=60°，结论是求∠EDF的度数．

    方案  因为∠DEB=∠DFB=90°，所以要求得∠EDF的度数，只要求出∠B即可．而∠B+∠C=180°，故只需知道∠C的度数即可．根据平行四边形的对角相等，得∠A=∠C．又∠AED=∠CFD=90°，在△ADE和△CDF中，易求∠ADE=∠CDF=30°，可求得∠A=∠C=60°．

实施  ∵四边形ABCD是平行四边形，

∴∠A=∠C，AD∥BC．

    ∴∠A+∠B=180°．

∵DE⊥AB，

∴∠A+∠ADE=90°．

同理∠C+∠CDF=90°．

    ∴∠ADE=∠CDF．

又∠ADE+∠CDF=60°，

∴∠ADE=∠CDF=30°，

∴∠A=60°．

    ∴∠B=180°-∠A=180°-60°=120°．

    在四边形DEBF中，∠DEB+∠B+∠BFD+∠FDE=360°，

    ∴∠EDF=360°-90°-120°-90°=60°．

    反思  （1）在平行四边形中，运用对角相等，邻角互补是解决角问题的重要条件．（2）在解决几何问题时，要善于挖掘图形的典型特征．

课时训练

1．在ABCD中，

  （1）若∠A=30°，则∠B=______，∠C=________，∠D=________．

  （2）若∠A：∠B=1：2，则∠A=______，∠B=_______，∠D=_______．

  （3）若∠A-∠B=40°，则∠A=______，∠B=_______．

  （3）若∠A+∠C=90°，则∠D=________．

2．如图，在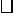ABCD中，下列各式不一定正确的是（  ）．

  （A）∠1+∠2=180°；（B）∠2+∠3=180°；

（C）∠3+∠4=180°；（D）∠2+∠4=180°