|
一、回顾与思考
1、学习(1)幂的意义a·a·……a=an
n个a相乘
(2)同底数幂的相乘法则am·an=am+n(m,n都是正整数)
二、创设情景,导入课题
1、课件展示乒乓球和足球的图片,先让学生直观体会两个球体的体积的大小的悬殊比例,然后让他们猜想足球的体积大约是乒乓球体积的多少倍?同学讨论、交流。最后,告诉他们足球的半径是乒乓球半径的几倍,让他们算足球的体积是乒乓球体积的多少倍?而导入新课。
2、,从计算的结果我们看出:球体的体积与半径的大小有着紧密的联系,如果甲球的半径是乙球的n倍,那么甲球的体积是乙球的体积n3倍。
地球、木星、太阳可以近似地看成球体,木星、太阳的半径分别约为地球的10倍和102倍,它们的体积约是地球的多少倍?
学生独立思考后回答:木星的体积是地球的体积的103倍,而太阳的体积则是地球的体积的(102)3。你知道(102)3到底是多少倍吗?猜想一下,并说明你的理由。
半径扩大的倍数与体积扩大的倍数哪个变化更大?这节课我们共同研究“幂的乘方”。
三、合作学习,建立模型
1、做一做
计算下列各式,并说明理由
(1)(102)3 (2)(34)2
(3)(a3)5 (4)(am)n
由学生合作完成,探索幂的乘方的法则的归纳过程,经小组讨论,交流各自的想法,看看别人是怎么运算出结果的,和自己的想法有何区别,最后指名让小组代表说自己的想法和运算过程及运算结果。
师生共同归纳为:
(1)(102)3=102×102×102(根据幂的意义)
=102+2+2(根据同底幂相乘法则)
=102×3
(2)(34)2=34×34=34+4=34×2=38
(3)(a3)5=a3·a3·a3·a3·a3=a3+3+3+3+3
=a3×5=a15
n个
(4)(am)n=am·am·am……am(幂的意义)
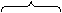 n个 n个
=a m+m+…+m(同底数幂相乘的法则)
=amn(乘法的意义)
2、总结法则
(am)n=amn(m,n都是正整数)
幂的乘方,底数不变,指数相乘。
3、想一想(小组讨论)
(am)n=与(an)m相等吗?为什么?
四、应用新知,体验成功
1、 例3:计算下列各式,采用幂的形式表示
(1)(107)3 (2)(a4)8 (3)[(-x)6]3
(4)-(x2)m (5)(x3)4·(x2)5
(6)2(a2)6-(a3)4
解:(1)(107)3=107×3=1021
(2)(a4)8=a4×8=a32
(3)[(-x)6]3=(-x)6×3=(-x)18=x18
(4)-(x2)m=-x2m
(5)(x3)4·(x2)5=x3×4·x2×5=x12·x10
=x12+10=x22
(6)2(a2)6-(a3)4=2a2×6-a3×4=2a12-a12=a12
2、 课内练习
详见教材P115页
1、口答; 2、改错; 3、计算
五、探索挑战,激发情智
1、探究活动
教材P116探究活动,探究魔方
2、智能挑战
在255,344,433,522,这四个幂的数值中,最大的一个是 344
六、归纳小结,充实结构
1、今天收获1,2,3……
2、结构
|
|
|
|
|
|
幂的乘方运算法则
(am)n=amn(m,n都是正整数)
底数不变,指数相乘 | |
|
 |
| 
幂
的
  意 意
同底数幂相乘法则:
am·an=am+n(m,n都是正整数)
底数不变,指数相加 | | 义
七、知识留恋,课后韵味
布置作业:课本后附作业题 |
充分的复习回顾与本节课有联系的认识,便于建构新知和理解法则之间的联系,对建构正确的模型大有好处。
设计从实际问题引入幂的乘方运算,学生在探索这个问题的过程中,将自然地体会幂的乘方运算的必要性,了解数学与现实世界的联系。
做一做的目的,是使学生通过对特例的考察,归纳幂的乘方的运算性质,并运用幂的意义加以说明,在此过程中,学生进一步体会了幂的意义,发展了归纳,符号演算等推理能力和有条理的表达能力。
推导法则时,显示理由,更能使学生进一步体会幂的意义。
通过小组讨论,更能辨别法则。
增添(4),是为了使学生对符号和底数有进一步的认识。
增添(6),提高综合运用的能力。
通过改错纠正,反思做题过程,深入理解法则的意义,达到融洽贯通。
魔方的探究能激起学生浓厚的学习兴趣,进一步体会幂的乘方法则。
挑战性问题能激发学生情智,从最近发展区理论出发,适当设置本课内容相关的挑战性问题对发展学生主动探索能力大有裨益。
开放式小结,充分地调动每一个学生的积极性
在小结中形式知识结构,便于学生理解和掌握。 | 
