|
1.5 三角形全等的条件(二)同步练习
【知识提要】
1.掌握边角边公理的内容.
2.能应用边角边公理证明两个三角形全等.
3.掌握线段垂直平分线的性质定理,并能应用它证明线段相等.
【学法指导】
1.边角边公理中相等的角必须是夹角,要注意两边及其中一边的对角对应相等的两个三角形不一定全等.
2.由边角边公理得出线段中垂线的性质定理,通过知识的纵横迁移感受数学的辩证特征.
 范例积累 范例积累
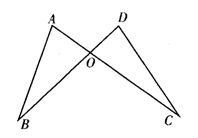
【例1】 如图1-5-16,BD、AC交于O,若OA=OD,用“SAS”证△AOB≌△DOC还需( )
A.AB=DC B.OB=OC
C.∠A=∠D D.∠AOB=∠DOC
【分析】 用“SAS”证全等有三个独立条件,已知OA=OD,显然还差两个,由AC、BD相交可得∠AOB与∠DOC是一对对顶角,第三个条件应该围绕夹角∠AOB、∠DOC找,显然OB与OC应是另一组夹边.
【解】 选B.
【例2】 如图,已知AB、CD相交于O,△ACO≌△BDO,AE=BF,试说明CE=FD.
【分析】 本题考查SAS公理的应用,要证CE=FD,只要证△OCE≌△ODF.显然∠EOC=∠FOD.需证OE=OF,OC=OD.因AE=BF,故需证OA=OB,由已知△ACO≌△BDO,可得OC=OD,OA=OB.
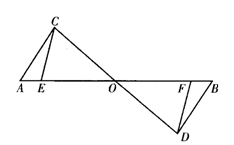 【解】 ∵△ACO≌△BDO 【解】 ∵△ACO≌△BDO
∴CO=DO,AO=BO
∵AE=BF,∴EO=FO
在△EOC与△FOD中 |

