|
2.1.4 函数的奇偶性 学案
【预习要点及要求】
1.函数奇偶性的概念;
2.由函数图象研究函数的奇偶性;
3.函数奇偶性的判断;
4.能运用函数奇偶性的定义判断函数的奇偶性;
5.理解函数的奇偶性。
【知识再现】
1.轴对称图形:
2中心对称图形:
【概念探究】
1、 画出函数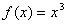 ,与 ,与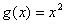 的图像;并观察两个函数图像的对称性。 的图像;并观察两个函数图像的对称性。
2、 求出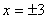 , ,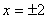 , ,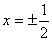 时的函数值,写出 时的函数值,写出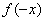 , ,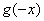 。 。
结论: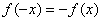 , ,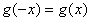 。 。
3、 奇函数:___________________________________________________
4、 偶函数:______________________________________________________
【概念深化】
(1)、强调定义中“任意”二字,奇偶性是函数在定义域上的整体性质。
(2)、奇函数偶函数的定义域关于原点对称。
5、奇函数与偶函数图像的对称性:
如果一个函数是奇函数,则这个函数的图像是以坐标原点为对称中心的__________。反之,如果一个函数的图像是以坐标原点为对称中心的中心对称图形,则这个函数是___________。
如果一个函数是偶函数,则这个函数的图像是以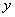 轴为对称轴的__________。反之,如果一个函数的图像是关于 轴为对称轴的__________。反之,如果一个函数的图像是关于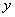 轴对称,则这个函数是___________。 轴对称,则这个函数是___________。
6. 根据函数的奇偶性,函数可以分为____________________________________.
【例题解析】 例1.已知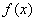 是奇函数 是奇函数 |

