|
2.3 函数的应用(一)学案
【预习达标】
1.形如f(x)= 叫一次函数,当 为增函数;当为减函数。
2.二次函数的解析式三种常见形式为 ;
; 。
3.f(x)=a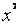 +bx+c(a +bx+c(a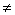 0),当a 0,其图象开口向 ,函数有最 值,为 ; 0),当a 0,其图象开口向 ,函数有最 值,为 ;
当a 0, 其图象开口向 ,函数有最 值,为 。(当给定一区间的二次函数的最值问题怎样考虑?)
4. f(x)=a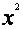 +bx+c(a +bx+c(a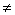 0)当a>0时,增区间为 ;减区间为 . 0)当a>0时,增区间为 ;减区间为 .
【典例解析】
例1.《民共和国个人所得税法》十四条中有表:
个人所得税税率表(工资 / 薪金所得使用)
|
级数 |
全月应纳税所得额 |
税率(%) |
|
1 |
不超过500元 |
5 |
|
2 |
超过500元至2000元的部分 |
10 |
|
3 |
超过2000元至5000元的部分 |
15 |
|
4 |
超过5000元至20000元的部分 |
20 |
|
5 |
超过20000元至40000元的部分 |
25 |
|
6 |
超过40000元至60000元的部分 |
30 |
|
7 |
超过60000元至80000元的部分 |
35 |
|
8 |
超过80000元至100000元的部分 |
40 |
|
9 |
超过100000元的部分 |
45 |
目前,上表中"全月应纳税所得额"是从工资薪金收入中减去800元后的余额.如,某人月工资薪金收入1320元,减去800元,应纳税所得额为520元,由税率表知其中500元税率为5%,另20元的税率为10%,所以此人应纳个人所得税500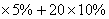 =27元. =27元.
(1) 请写出月工资薪金的个人所得税y关于工资薪金收入x(0<x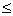 10000) 10000) 的函数表达式; 的函数表达式;
(2) 某人在某月交纳的个人所得税是120元,他那个月的工资薪金收入是多少?
|

