|
2.4.1 函数的零点 教案
教学目标:
1、知识目标:理解函数零点的意义,能判断二次函数零点的存在性,会求简单函数的零点,了解函数的零点与方程根的关系 .
2、能力目标:体验函数零点概念的形成过程,引导学生学会用转化与数形结合思想方法研究问题,提高数学知识的综合应用能力.
3、情感目标:让学生初步体会事物间相互转化以及特殊到一般的辨证思想.
重点、难点:
教学过程:
一.自主达标
1.如果函数y=f(x)在实数处的值等于零,即f(x)=0,则x叫做 .
2.把一个函数的图像与 叫做这个函数的零点.
3.二次函数y=a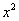 +bx+c(a +bx+c(a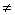 0),当 0),当
Δ=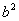 -4ac>0时,二次函数有 个零点; -4ac>0时,二次函数有 个零点;
Δ=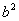 -4ac=0时,二次函数有 个零点; -4ac=0时,二次函数有 个零点;
Δ=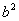 -4ac<0时,二次函数有 个零点. -4ac<0时,二次函数有 个零点.
4.二次函数零点的性质:
(1)二次函数的图像是连续的,当它通过零点时(不是二重零点),
.
(2)在相邻的两个零点之间所有 .
二。典例解析
例1.若函数f(x)=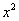 +ax+b的两个零点是2和-4,求a,b的值. +ax+b的两个零点是2和-4,求a,b的值.
例1、解:函数f(x)=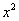 +ax+b的两个零点是2和-4,也就是方程 +ax+b的两个零点是2和-4,也就是方程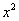 +ax+b=0的两个根是2和-4,由根与系数的关系可知 +ax+b=0的两个根是2和-4,由根与系数的关系可知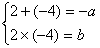 得a=2,b=-8. 得a=2,b=-8.
评析:反常的根与函数零点的关系以及反常的根与系数的关系是本体解决关键. 例2.求证:方程5 |

