|
2.1.1 函数 学案(2)
【预习要点及要求】
1.映射的概念,映射与函数的关系.
2.了解映射,一一映射的概念,初步了解映射与函数间的关系.以判定一些简单的映射.
【知识再现】
1、函数的定义:___________________________________
2、函数的定义域、值域:___________________________________
3、区间的概念:___________________________________
【概念探究】
1、映射的概念
设A、B是两个非空集合,如果按照某种对应法则f,对A内任意一个元素x,在B中 一个元素y与x对应,则称f是集合A到B的 .这时称y是x在映射f的作用下的 ,记作f(x).于是y=f(x)中x称做y的 .
2、集合A到B的映射f可记为f:A→B或x→f(x).其中A叫做映射f的 (函数定义域的推广),由所有象f(x)构成的集合叫做映射f的 ,通常记作f(A).
3、如果映射f是集合A到B的映射,并且对于B中的任何一个元素,在集合A中都有且只有一个原象,这时我们说这两个集合之间存在 ,并称这个映射为集合A到集合B的 .
4、由映射的定义可以看出,映射是 概念的推广, 是一种特殊的映射,要注意构成函数的两个集合A、B必须是 .
完成课本P34-35,例4、例5、例6、例7.
【总结点拨】
从集合A到集合B的映射,允许多个元素对应一个元素,而不允许一个元素对应多个元素.
【例题讲解】
例1、判断下列对应哪些是由A到B的映射?为什么?
(1)A=R,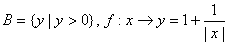 ; ;
(2)A=R,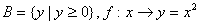 ; ;
(3)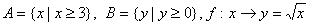 (4)A=Z,B=Q, (4)A=Z,B=Q,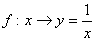
例2、已知集合A= |

