|
3.2.2半角的正弦、余弦和正切
(一)教学目标
1. 知识目标:掌握公式及其推导过程,会用公式进行化简、求值和证明。
2. 能力目标:通过公式推导,掌握半角与倍角之间及半角公式与倍角公式之间的联系, 培养逻辑推理能力。
3. 情感目标:培养用联系的观点看问题的观点。
(二)教学重点、难点
本节重点是公式的推导与应用,难点是半角与倍角的联系及符号的判断。
(三)教学方法
观察、归纳、启发、探究相结合的教学方法。
(四)教学过程
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
|
复习引入 |
复习倍角公式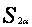 、 、 、 、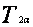 |
先让学生默写三个倍角公式,注意等号两边角的关系,特别注意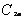 。既然能用单角表示倍角,那么能否用倍角表示单角呢? 。既然能用单角表示倍角,那么能否用倍角表示单角呢? |
以旧引新,设疑创设情境,引导学生展开积极的思维活动 |
|
半角公式的推导及理解 |
推导半角公式: |
由学生根据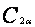 推导,老师巡视并帮助有困难的学生,之后对照课本P145检查过程和结果。 推导,老师巡视并帮助有困难的学生,之后对照课本P145检查过程和结果。
思考讨论:
①公式是如何推导出来的?有何限制条件?
②公式有何特点?如何记忆?
③公式如何变形?有何用处?
先有学生回答问题,然后老师明确,结论如下:
① 由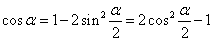
得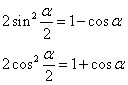
所以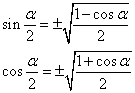
两式相除得
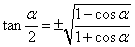 ( (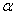 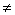 (2k+1) (2k+1) 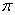 ) )
②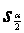 与 与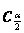 结构相同,一号之差, 结构相同,一号之差,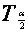 是由 是由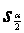 与 与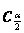 推出的 推出的
③ 平方后是降幂公式,用于变形、求值、证明
|
培养学生运用已有知识获得新知识的能力和问题探究的能力,同时也使学生认识到了新公式的来源。通过讨论,使学生对公式有一个清晰完整的认识,为公式的灵活应用打下基础,逐步培养自学能力。 | |

