|
v
课题 最简三角方程
上海市延安中学 吕志勇
一、教案设计思考
这节课的内容是给出三角方程的定义,以及解最简三角方程的基本方法,其中要应用到三角函数性质及图像、反三角函数、诱导公式等知识,还包括数形结合、转换、分类讨论、类比等数学思想方法,是对所学过的许多三角知识进行应用,在三角比和三角函数这两章内容中的地位还比较重要,它是先有三角比值,然后要研究满足这样的条件的角是什么,也完善了解三角形的理论基础.
这节课用解三角形时的一个问题来引入,简单并能引起同学的兴趣,然后整节课采用启发、探究的教学方法,调动同学积极思考问题.
二、教学目标
理解三角方程、最简三角方程的定义,掌握三种最简三角方程的解法;体会由特殊到一般的研究问题的方法,能综合运用所学知识解决问题,能用数形结合、转换、分类讨论、类比等数学思想方法解决有关问题.
三、教学重点、难点
解三角方程的思想方法
四、教学方法和手段
采用启发式教学模式
五、教学过程
1、引入
前面我们重点学习了三角函数的有关知识,研究了角的变化对三角比值的影响,在解三角形中我们已经遇到知道了一个角的三角比值,要求这个角,如知道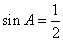 ,由于角 ,由于角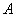 是三角形中的内角,所以有 是三角形中的内角,所以有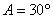 或 或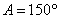 ,今后我们会遇到类似的问题,特别是当角 ,今后我们会遇到类似的问题,特别是当角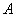 的大小没有条件限制时,那么满足 的大小没有条件限制时,那么满足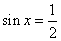 的 的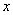 有多少呢?我们把这样的方程叫做三角方程,那么如何解这类方程呢?下面就请同学思考这个问题. 有多少呢?我们把这样的方程叫做三角方程,那么如何解这类方程呢?下面就请同学思考这个问题.
2、探究
要研究如何解三角方程,先解决较简单的方程,就以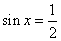 为例,同学思考后,进行交流讨论. 为例,同学思考后,进行交流讨论.
同学1:这个方程应该有无数多个解,但还没有找到解决的方法. 同学2: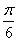 和 和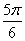 都是方程的解,又函数 都是方程的解,又函数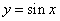 的最小正周期是 的最小正周期是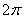 ,所以此方程的解集是 ,所以此方程的解集是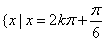 或 或 |

