|
§2 集合的基本关系
教材分析:类比实数的大小关系引入集合的包含与相等关系
了解空集的含义
课 型:新授课
教学目的:(1)了解集合之间的包含、相等关系的含义;
(2)理解子集、真子集的概念;
(3)能利用Venn图表达集合间的关系;
(4)了解与空集的含义。
教学重点:子集与空集的概念;用Venn图表达集合间的关系。
教学难点:弄清元素与子集 、属于与包含之间的区别;
教学过程:
观察以下几组集合,并指出它们元素间的关系:
① A={1,2,3}, B={1,2,3,4,5}; ② A={x | x>1}, B={x | x2>1};
③ A={四边形}, B={多边形}; ④ A={x | x2+1=0}, B={x | x > 2} .
1. (子集) 定 义
一般地,对于两个集合A与B,如果集合A中的任何一个元素都是 集合B的元素,我们就说集合A包含于集合B,或集合B包含集合A.
记作 : 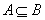 (或 (或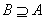 ),也说集合A是集合B的子集. ),也说集合A是集合B的子集.
练习:判断集合A是否为集合B的子集,若是则在( )打√,若不是则在( )打×:
①A={1,3,5}, B={1,2,3,4,5,6} ( √ ) ② A={1,3,5}, B={1,3,6,9} ( × )
③A={0}, B={x | x2+2=0} ( × ) ④ A={a,b,c,d}, B={d,b,c,a} ( √ )
2. (相等) 定 义
一般地,对于两个集合A与B,如果集合A中的任何一个元素都是集合B的元素,同时集合B中的任何一个元素都是集合A的元素,则称集合A等于集合B,
记作 : 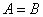
若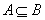 且 且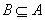 ,则 ,则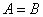 ;反之,亦然。 ;反之,亦然。
观察集合A与集合B的关系:
(1) A={a,b,c,d}, B={d,b,c,a}
(2) A={-1,1}, B={x | x2-1=0}
|

