|
1. 初步掌握“立几”中“探索性” “发散性”等命题的解法.
2.能正确地分析出几何中基本元素及其相互关系.能对图形进行分解、组合和变形.
 进一步提高空间想象能力和逻辑思维能力. 进一步提高空间想象能力和逻辑思维能力.
二. 课前预习
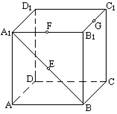
1. 棱长为1的正方体容器ABCD-A1B1C1D1 , 在A1B、A1B1、
B1C1的中点E、F、G处各开有一个小孔. 若此容器可以
任意放置, 则装水最多的容积是 ( )
(小孔面积对容积的影响忽略不计)
 A. A. 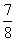 B. B. 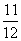 C. C. 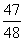 D. D. 
2.如图,是一个无盖的正方体盒子展开后的平面图, A、B、C是展
开图上的三点, 则正方体盒子中∠ABC的值为 ( )
A.180° B. 120°
C.60° D. 45°
3.图中多面体是过正四棱柱的底面正方形ABCD的点A作截
面AB1C1D1而截得的, 且BB1=DD1已知截面AB1C1D1与底面ABCD成30°
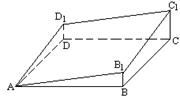 的二面角, 则这个多面体的体积 ( ) 的二面角, 则这个多面体的体积 ( )
A.  B. B. 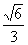
|

