|
2011年高考第二轮专题复习(教学案):立体几何
第1课时 直线、平面、空间几何体
考纲指要:
立体几何在高考中占据重要的地位,考察的重点及难点是直线与直线、直线与平面、平面与平面平行的性质和判定,而查空间线面的位置 关系问题,又常以空间几何体为依托,因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式。 关系问题,又常以空间几何体为依托,因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式。
考点扫描:
1.空间两条直线的位置关系:(1)相交直线;(2)平行直线;(3)异面直线。
2.直线和平面的位置关系:(1)直线在平面内;(2)直线和平面相交;(3)直线和平面平行。
3.两个平面的位置关系有两种:(1)两平面相交;(2)两平面平行。
4.多面体的面积和体积公式,旋转体的面积和体积公式。
考题先知:
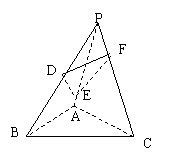 例1.在平面几何中,我们学习了这样一个命题:过三角形的内心作一直线,将三角形分成的两部分的周长比等于其面积比。请你类比写出在立体几何中,有关四面体的相似性质,并证之。 例1.在平面几何中,我们学习了这样一个命题:过三角形的内心作一直线,将三角形分成的两部分的周长比等于其面积比。请你类比写出在立体几何中,有关四面体的相似性质,并证之。
解:通过类比,得命题:过四面体的内切球的球心作一截面,将四面体分成的两部分的表面积比等于其体积比。
证明:如图,设四面体P-AB C的内切球的球心为O,过O作截面DEF交三条棱于点E、D、F,记内切圆半径为r,则r也表示点O到各面的距离,利用体积的“割补法”知: C的内切球的球心为O,过O作截面DEF交三条棱于点E、D、F,记内切圆半径为r,则r也表示点O到各面的距离,利用体积的“割补法”知:
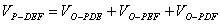 = =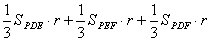
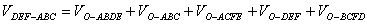
=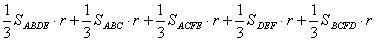 ,从而 ,从而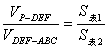 。 。 例2.( |

