|
8.正方形
知识考点:
理解正方形的性质和判定,并能利用它进行有关的证明和计算。
精典例题:
【例1】如图,E、F分别是正方形ABCD的边AB、BC上的点,且EF∥AC,在DA的延长线上取一点G,使AG=AD,EG与DF相交于点H。求证:AH=AD。
分析:因为A是DG的中点,故在△DGH中,若AH=AD,当且仅当△DGH为直角三角形,所以只须证明△DGH为直角三角形(证明略)。
评注:正方形除了具备平行四边形的一般性质外,还特别注意其直角的条件。本例中直角三角形的中线性质使本题证明简单。
 
【例2】如图,在正方形ABCD中,P、Q分别是BC、CD上的点,若∠PAQ =450,求证:PB+DQ=PQ。 =450,求证:PB+DQ=PQ。
分析:利用正方形的性质,通过构造全等三角形来证明。
变式:若条件改为PQ=PB+DQ,那么∠PAQ=?你还能得到哪些 结论? 结论?
探索与创新:
【问题一】如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,过A作AG⊥EB于G,AG交BD于点F,则OE=OF,对上述命题,若点E在AC的延长线上,AG⊥EB,交EB的延长线于点G,AG的延长线交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,说明理由。
 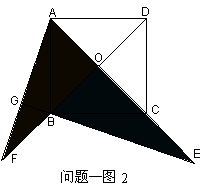
分析:对于图1通过全等三角形证 |

