|
17.相似形的综合运用(一)
知识考点:
会综合运用相似三角形的有关概念、定理解答有关问题。另外,直角三角形被斜边上的高分成的两个直角三角形与原三角形相似的性质运用,是近几年中考的热点题型。
精典例题:
【例1】如图,已知,在边长为1的正方形ABCD的一边上取一点E,使AE=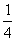 AD,从AB的中点F作HF⊥EC于H。 AD,从AB的中点F作HF⊥EC于H。
(1)求证:FH=FA;
(2)求EH∶HC的值。
证明:(1)连结EF,F C,在正方形ABCD中,AD=AB=BC,∠A=∠ C,在正方形ABCD中,AD=AB=BC,∠A=∠ B=900 B=900
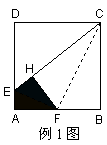 ∵ ∵ AE= AE=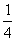 AD,F为AB的中点,∴ AD,F为AB的中点,∴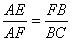
∴△EAF∽△FBC,∴∠AEF=∠BFC,∠EFA=∠CFB
∴∠EFC=900,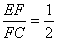
又∵∠EFC=∠B=900 ∴△EFC∽△FBC
∴∠HEF=∠BFC,∠ECF=∠BCF
∴∠AEF=∠HEF,∠AFE=∠HFE
∴△EAF≌△HEF ∴FH=FA
 (2)由(1)得 (2)由(1)得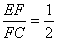 ,由(1)易证△EHF∽△EFC,从而可得 ,由(1)易证△EHF∽△EFC,从而可得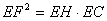 ,同理 ,同理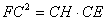 ,于是 ,于是 EH∶HC= EH∶HC=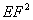 ∶ ∶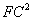 =1∶4 =1∶4
变式:如图,在矩形ABCD中,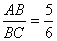 ,点E在BC上,点F在CD上,且EC= ,点E在BC上,点F在CD上,且EC=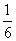 BC,FC= BC,FC=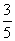 C C D,FG⊥AE于G,。求证:AG=4GE。 D,FG⊥AE于G,。求证:AG=4GE。
(提示:证△ECF∽△FDA得EF∶AF=1∶2,再证△EFG∽△EAF∽△FAG即可) 【例2】已知,在△ABC中,∠ACB=900,过C作CD⊥AB于D,AD=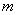 ,BD= ,BD=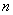 , ,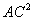 ∶ ∶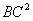 =2∶1,又 =2∶1,又 |

