|
涉及高中知识的阅读理解中考题
阅读理解型问题是中考的一个重要考点,涉及高中知识的中考题各地中考试卷中频繁出现,值得重视。本文就这类题的特点及解法举例说明。
例1(2003年·广西)阅读下列一段话,并解决下面的问题。
观察这样一列数:1,2,4,8,……我们发现这一列数从第2项起,每一项与它前一项的比都等于2。一般地,如果一列数从第2项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数叫做等比数列的公比。
(1)等比数列5,-15,45,……的第4项是______________;
(2)如果一列数a1,a2,a3,a4,…是等比数列,且公比为q,那么根据上述的规定,有
所以,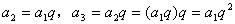 , ,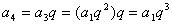 ,… ,…
an=_________。(用a1与q的代数式表示)
(3)一等比数列的第2项是10,第3项是20,求第1项与第4项。
解:(1)-135;(2)
(3)因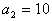 , ,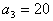 ,故 ,故
因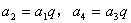 ,故 ,故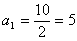 , ,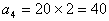
评析:本题取材于高中代数中的等比数列,既能考查学生的理解运用能力,又能够锻炼学生的自学能力,引导学生养成良好的探索习惯。
例2 (2003年·甘肃省)平面上有n个点(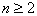 ),且任意3点不在同一直线上,过这些点作直线,一共能作出多少条不同的直线? ),且任意3点不在同一直线上,过这些点作直线,一共能作出多少条不同的直线?
分析:当仅有2个点时,可连成1条直线;有3个点时,可连成3条直线;有4个点时,可连成6条直线;有5个点时,可连成10条直线;……
归纳:考察点的个数n和可连成直线的条数Sn,发现规律如表1。
表1

推理:平面上有n个点,两点 |

