|
函数的应用
班级 姓名 学号
一、知识目标
1.能根据实际问题中的变量之间的关系,确定函数关系式,解决实际问题.
2.能主动从表格或图象中获取有用信息,用一次函数或反比例函数解决问题.
二、典型例题
1.如图,一束光线从y轴上点A(0,2)出发,经过x轴上点C反射后经过点B(6,6),则光线从点A到点B所经过的路程是 ( )
 A.10 B.8 C.6 D.4 A.10 B.8 C.6 D.4
2.若反比例函数 图象上有一点P(a,b) 且PA⊥x轴于A, S△PAO=3,则k=_______.
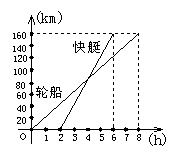 反比例函数解析式为:_________________. 反比例函数解析式为:_________________.
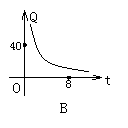
3.如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象( 分别是正比例函数图象和一次函数图象).根据图象解答下列问题:
(1)请分别求出表示轮船和快艇行驶过程的函数解析式
(2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少?
(3)问快艇出发多长时间赶上轮船?
分析:由已知条件可设两条直线分别为y=k1x(k1≠0)或y=k2x+b(k2≠0),然后根据图象给出的点的坐标,利用“待定系数法”可确定(1)中的两条直线;(2)由图可得轮船8h行160km,快艇4h行160km,分别求其速度;(3)根据追及问题中“快者路程- 相距路程=慢者路程”可求解.
点评:本题主要通过一次函数图象与坐标轴的交点的意义来解决实际问题,因此弄清交点的意义是关键,然后用待定系数法求函数解析式.
三、课堂练习:
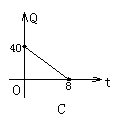
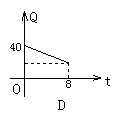
1.拖拉机开始工作时,油箱中有油40L,如果每小时耗油5L, 那么工作时,油箱中的余油量Q(L)与工作时间t(h)的函数关系用图象可表示为( )
 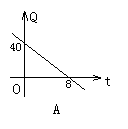  
2.在某一段电路中,保持电压不变,则电流强度I |

