|
全等三角形
 一、下列各题已有解答的有“病”吗?如果有“病”,请写出“病因”。没有解答的,你认为易让别人犯错的“陷阱”在哪儿? 一、下列各题已有解答的有“病”吗?如果有“病”,请写出“病因”。没有解答的,你认为易让别人犯错的“陷阱”在哪儿?
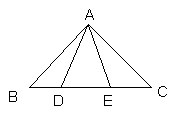
1.已知△ABD≌△ACE,求证:△ABE≌△ACD
证明:∵△ABD≌△ACE
∴△ABD+△ADE≌△ACE+△ADE ∴△ABE≌△ACD
▲错因分析或陷阱是
▲正确解答是:
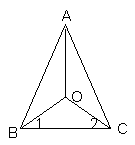
2.如图,AO平分∠BAC,∠1=∠2 求证:△ABC是等腰三角形
证明:∵∠1=∠2 ∴ OB=OC
∵AO平分∠BAC ∴∠BAO=∠CAO
在△AOB≌△AOC中∵OB=OC 、∠BAO=∠CAO 、OA=OA
∴△AOB≌△AOC ∴AB=AC ,即△ABC是等腰三角形
▲错因分析或陷阱是
▲正确解答是:
3.两边和第三边上的高对应相等相等的两个三角形全等(判断)
解:通过两次全等,可以证明这个命题是正确的
▲错因分析或陷阱是_____________________________________________________
▲正确解答是___________________________________________________________
二、“全等三角形”给你留下多少?尝试填写下列知识点(并在脑海中构建知识体系)
1、 叫全等三角形
2、全等三角形的性质:全等三角形的对应边 、全等三角形的对应角 、
全等三角形的对应边上的高 、全等三角形的对应边上的中线 、全等三角形的对应角的平分线
3、三角形全等的判定方法:
(1) 的两个三角形全等(简记为 SSS )
(2) 的两个三角形全等(简记为 SAS )
(3) 的两个三角形全等(简记为 ASA )
(4) 的两个三角形全等(简记为 AAS )
(5) 的两个三角形全等(简记为 HL )
4、满足下面的条件的两个三角形也是全等的: (1)有两边和其中一边上的中线对应相等的两个三 |

