|
锐角三角函数
班级 姓名 学号
教学目标
1. 知道三个三角函数的定义,了解三角函数的值随锐角度数的变化规律;明白三角函数的值与角的大小有关,而与位置及边长无关.
2. 会计算含特殊角的三角函数式子的值,会根据已知三角函数值求相应的锐角;能解直角三角形.
3.  在解题过程中,学会划归、数形结合等数学思想. 在解题过程中,学会划归、数形结合等数学思想.
教学设计
一、知识回顾
1.知识点填
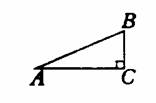
(1)定义:如图, ∠C=90°,sinA= ,cosA= , =.
(2)特殊角的三角函数值.
|
a |
sina |
cosa |
tana |
|
30° |
|
|
|
|
45° |
|
|
|
|
60° |
|
|
|
(3)若∠A是锐角,则 <sinA< , <cosA< ;
正弦、正切值是随着角度的增大而 ,余弦是随着角度的增大而 .
2.判断
(1)在Rt△ABC中, ∠C=90°,若两条直角边的长都扩大为3倍,则tan A也扩大为3倍. ( )
(2) sin60°=2 sin30°. ( )
(3)在Rt△ABC中, ∠C=90°,则sinA=cosB. ( )
3.选择
(1)已知cosα<0.5,那么锐角α的取值范围 ( )
A、60°<α<90° B、 0°< α <60°
C、30°<α<90° D、 0°< α <30°
 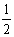 (2)如果√cosA – + | tanB –3|=0 (2)如果√cosA – + | tanB –3|=0
那么△ABC是 ( )A、直角三角形 B、锐角三角形
C、钝角三角形 D、等边三角形 (3)某市在“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境.已知这种草皮每平方米售价30元,则购买这种草皮至 |

