|
2011年普通高等学校全国统一考试(山东卷)
理科数学
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的的四个选项中,只有一个项是符合题目要求的。
(1)设集合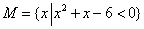 , ,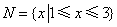 ,则 ,则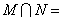
A.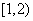 B. B. 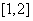 C. C. 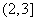 D. D. 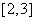
解析: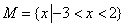 , ,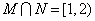 ,答案应选A。 ,答案应选A。
(2)复数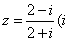 为虚数单位)在复平面内对应的点所在的象限为 为虚数单位)在复平面内对应的点所在的象限为
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解析: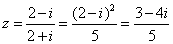 对应的点为 对应的点为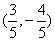 在第四象限,答案应选D. 在第四象限,答案应选D.
(3)若点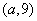 在函数 在函数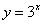 的图象上,则 的图象上,则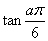 的值为 的值为
A.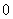 B. B. 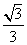 C. C. 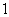 D. D. 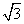
解析: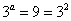 , ,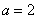 , , ,答案应选D. ,答案应选D.
(4)不等式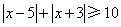 的解集是 的解集是
A.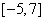 B. B. 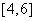 C. C. 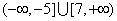 D. D. 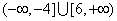
解析:当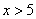 时,原不等式可化为 时,原不等式可化为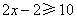 ,解得 ,解得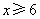 ;当 ;当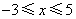 时,原不等式可化为 时,原不等式可化为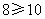 ,不成立;当 ,不成立;当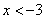 时,原不等式可化为 时,原不等式可化为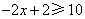 ,解得 ,解得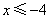 .综上可知 .综上可知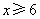 ,或 ,或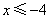 ,答案应选D。 ,答案应选D。
另解1:可以作出函数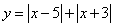 的图象,令 的图象,令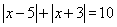 可得 可得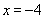 或 或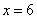 ,观察图像可得 ,观察图像可得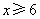 ,或 ,或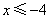 可使 可使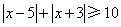 成立,答案应选D。 成立,答案应选D。
另解2:利用绝对值的几何意义,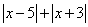 表示实数轴上的点 表示实数轴上的点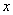 到点 到点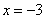 与 与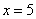 的距离之和,要使点 的距离之和,要使点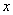 到点 到点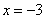 与 与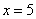 的距离之和等于10,只需 的距离之和等于10,只需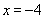 或 或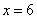 ,于是当 ,于是当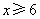 ,或 ,或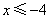 可使 可使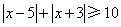 成立,答案应选D。 成立,答案应选D。
(5)对于函数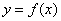 , , ,“ ,“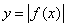 的图象关于 的图象关于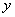 轴对称”是“ 轴对称”是“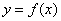 是奇函数”的 是奇函数”的
A充分不必要条件 B.必要不充分条件 C.充要条件 D.即不充分也不必要条件
解析:若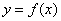 是奇函数,则 是奇函数,则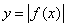 的图象关于 的图象关于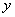 轴对称;反之不成立,比如偶函数 轴对称;反之不成立,比如偶函数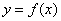 ,满足 ,满足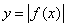 的图象关于 的图象关于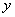 轴对称,但不一定是奇函数,答案应选B。 轴对称,但不一定是奇函数,答案应选B。
(6)若函数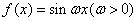 在区间 在区间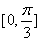 上单调递增,在区间 上单调递增,在区间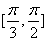 上单调递减,则 上单调递减,则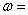
A.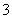 B. B. 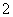 C. C. 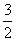 D. D. 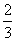
解析:函数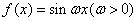 在区间 在区间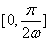 上单调递增,在区间 上单调递增,在区间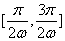 上单调递减, 上单调递减,
则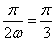 ,即 ,即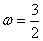 ,答案应选C。 ,答案应选C。
另解1:令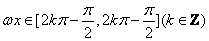 得函数 得函数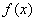 在 在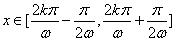 为增函数,同理可得函数 为增函数,同理可得函数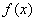 在 在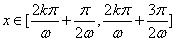 为减函数,则当 为减函数,则当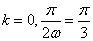 时符合题意,即 时符合题意,即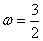 ,答案应选C。 ,答案应选C。
另解2:由题意可知当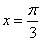 时,函数 时,函数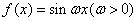 取得极大值,则 取得极大值,则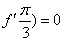 ,即 ,即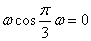 ,即 ,即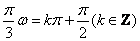 ,结合选择项即可得答案应选C。 ,结合选择项即可得答案应选C。
另解3:由题意可知当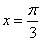 时,函数 时,函数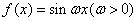 取得最大值, 取得最大值,
则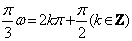 , ,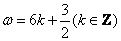 ,结合选择项即可得答案应选C。 ,结合选择项即可得答案应选C。 |

