|
21.2 二次根式的乘除
第1课时
【教学内容】
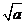 · ·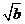 = =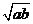 (a≥0,b≥0),反之 (a≥0,b≥0),反之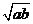 = =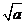 · ·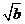 (a≥0,b≥0)及其运用. (a≥0,b≥0)及其运用.
【教学目标】
1、知识与技能
理解二次根式的乘法法则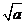 · ·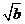 = =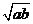 (a≥0,b≥0),及其逆用 (a≥0,b≥0),及其逆用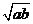 = =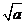 · ·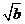 (a≥0,b≥0),并能利用它们进行计算和化简 (a≥0,b≥0),并能利用它们进行计算和化简
2、过程与方法
通过比较、猜想、论证二次根式的乘法运算法则,通过计算和化简掌握二次根式的乘法运算法则。
由具体数据,发现规律,导出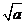 · ·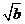 = =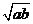 (a≥0,b≥0)并运用它进行计算;利用逆向思维,得出 (a≥0,b≥0)并运用它进行计算;利用逆向思维,得出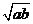 = =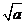 · ·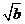 (a≥0,b≥0)并运用它进行解题和化简. (a≥0,b≥0)并运用它进行解题和化简.
3、情感、态度与价值观
通过二次根式的计算与化简,培养学生对根式的运算兴趣,并掌握运算的技巧
【教学重难点关键】
重点:
二次根式的乘法运算和化简.
难点:
发现规律,导出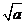 · ·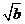 = =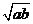 (a≥0,b≥0)以及它的双向使用 (a≥0,b≥0)以及它的双向使用
关键:
注意双向使用,讲清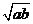 在a<0,b<0时的运算,如 在a<0,b<0时的运算,如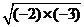 = = = =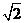 × ×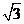 . .
【教学过程】
一、创设情境,导入新课
(学生活动)请同学们完成下列各题.
1. 二次根式有哪些性质?
2、现有一个长为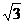 cm,宽为 cm,宽为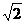 cm的长方形的面积是多少? cm的长方形的面积是多少?
3、二次根式可以进行平方运算,它还可以进行其他的运算,如:加减运算、乘除运算吗?
二、合作交流,探索新知
1、二次根式的乘法
[探究] 填空,观察结果,发现有什么规律?
(1)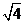 × ×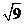 =_______, =_______,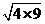 =______; =______;
(2)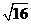 × ×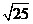 =_______, =_______,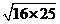 =________. =________.
(3)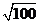 × ×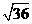 =________, =________,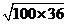 =_______. =_______.
参考上面的结果,用“>、<或=”填空.
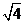 × ×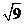 _____ _____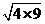 , ,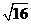 × ×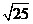 _____ _____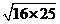 , ,
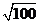 × ×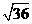 ________ ________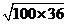
[进一步探究]利用你发现的规律填空,并利用计算器检验
(1)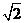 × ×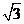 ______ ______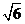 ,(2) ,(2)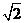 × ×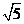 ______ ______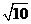 , ,
(3)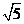 × ×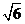 ______ ______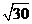 ,(4) ,(4)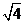 × ×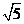 ______ ______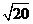 , ,
(5)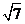 × ×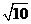 ______ ______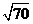 . .
老师点评(纠正学生练习中的错误)(1)被开方数都是正数;2)两个二次根式的乘除等于一个二次根式,并且把这两个二次根式中的数相乘,作为等号另一边二次根式中的被开方数.
[猜想] 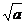 · ·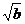 = =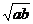 (a≥0,b≥0) (a≥0,b≥0)
一般地,对二次根式的乘法规定为
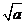 · ·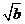 = =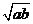 .(a≥0,b≥0) .(a≥0,b≥0) |

