机车启动之三最
1. 机车起动的最大速度
机车的速度达到最大时,一定是机车的加速度为零.弄清了这一点,利用平衡条件就很容易求出机车的最大速度.
例1 (09年高考上海卷)质量为5×103kg的汽车在t=0时刻速度v0=10m/s,随后以P=6×104W的额定功率沿平直公路继续前进,经72s达到最大速度,设汽车受恒定阻力,其大小为2.5×103N.求:(1)汽车的最大速度vm;(2)汽车在72s内经过的路程s.
解析:汽车以恒定功率起动时,它的牵引力F将随速度v的变化而变化,其加速度a也随之变化,具体变化过程可采用如下示意图表示:
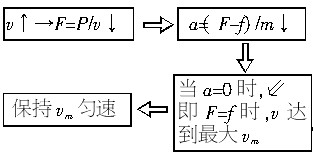
(1)当达到最大速度时,P=Fv=fvm,
所以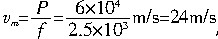
(2)从开始到72s时刻依据动能定理得:
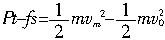
,解得: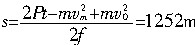
2. 机车匀加速起动的最长时间
机车匀加速度运动能维持的时间,一定是机车功率达到额定功率的时间.弄清了这一点,利用牛顿第二定律和运动学公式就很容易求出机车匀加速度运动能维持的时间.
例2 汽车发动机额定功率为60kW,汽车质量为5.0×103kg,汽车在水平路面行驶时,受到的阻力大小是车重的0.1倍,试求:若汽车从静止开始,以0.5 m/s2的加速度匀加速运动,则这一加速度能维持多长时间?
解析:要维持汽车加速度不变,就要维持其牵引力不变,汽车功率将随v增大而增大,当P达到额定功率P额后,不能再增加,即汽车就不可能再保持匀加速运动了.具体变化过程可用如下示意图表示:
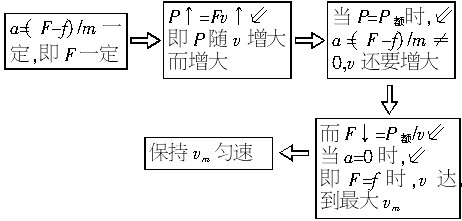
所以,汽车达到最大速度之前已经历了两个过程:匀加速和变加速,匀加速过程能维持到汽车功率增加到P额的时刻,设匀加速能达到最大速度为v1,则此时
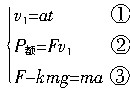 代入数据可得:t=16s 代入数据可得:t=16s
3. 机车运动的最大加速度
机车的额定功率一定时,机车运动的最大加速度是由机车的最大牵引力决定的,而最大牵引力是由牵引物的速度决定的.弄清了这一点,利用牛顿第二定律就很容易求出机车运动的最大匀加速度.
例3 电动机通过一绳子吊起质量为8kg的物体,绳的拉力不能超过120N,电动机的功率不能超过1200W,要将此物体由静止起用最快的方式吊高90 m(已知此物体在被吊高接近90m时,已开始以最大速度匀速上升)所需时间为多少?
解析:此题可以用机车启动类问题的思路,即将物体吊高分为两个过程处理:第一过程是以绳所能承受的最大拉力拉物体,使物体以最大加速度匀加速上升,第一个过程结束时,电动机刚达到最大功率.第二个过程是电动机一直以最大功率拉物体,拉力逐渐减小,当拉力等于重力时,物体开始匀速上升.
在匀加速运动过程中加速度为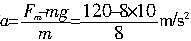
=5m/s2,末速度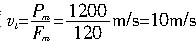
上升的时间t1=vt/a=2 s,上升高度为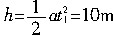
在功率恒定的过程中,最后匀速运动的最大速率为
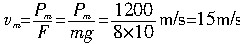
外力对物体做的功W=Pmt2-mgh2,动能变化量为

由动能定理得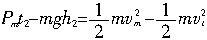
代入数据后解得t2=5.75s,所以t=t1+t2=7.75s即所需时间至少为7.75s. |

