不同运动中速度分解的妙方
速度的正交分解这一知识点常常“隐形”的渗透到不同运动方向的两个或多个连结体运动的情景中,或者运动物体的速度瞬间发生突变时的情景中。下面例举几道常出现速度分解的典型例题加以讨论分析,把握此知识点出现的规律性,以便灵活、准确的应用。
1.超重、失重物理情景中的速度分解
例1. 如图1,在不计滑轮摩擦和绳质量的条件下,当小车匀速向右运动时,物体A的受力情况是( )
A. 绳的拉力大于A的重力
B. 绳的拉力等于A的重力
C. 绳的拉力小于A的重力
D. 拉力先大于A的重力,后小于重力
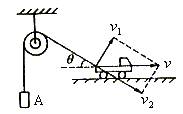
图1
解析:此类问题通常是通过定滑轮造成绳子两端的连接体运动方向不一致,导致主动运动物体和被动运动物体的加速、减速的不一致性。解答时必须运用两物体的速度在各自连接处绳子方向投影相同的规律。
把小车的速度为合速度进行分解,即根据运动效果向沿绳的方向和与绳垂直的方向进行正交分解,分别是v2、v1。如图1所示,题中物体A的运动方向与连结处绳子的方向相同,不必分解。A的速度等于v2,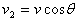 ,小车向右运动时, ,小车向右运动时,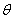 逐渐变小,可知 逐渐变小,可知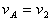 逐渐变大,故A向上做加速运动,处于超重状态,绳子对A的拉力大于重力,故选项A正确。 逐渐变大,故A向上做加速运动,处于超重状态,绳子对A的拉力大于重力,故选项A正确。
2.杆的各点运动速度不同的情景中的速度分解
例2. 如图2所示,当放在墙角的均匀直杆A端靠在竖直墙上,B端放在水平地面,滑到图示位置时,B点的速度为v,则A点的速度是________(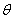 为已知)。 为已知)。
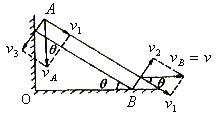
图2
解析:由于杆AB下滑时各点的速度不同,但各点速度沿杆方向的投影相同,即沿杆方向的速度效果相同,所以把两端点的速度必须向沿杆方向上和杆垂直的方向上正交分解。
把A、B两端点的速度为vA、vB各自做为合速度向沿杆AB的方向和与杆垂直的方向进行正交分解,如图2所示,沿杆AB方向的投影分速度相同,都是v1,那么有: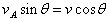 ,即求解出A下滑的速度: ,即求解出A下滑的速度: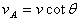 。 。
3.水平面内圆周运动的物理情景中的速度分解
例3. 如图3,一个小球被绳子牵引在光滑的水平板上,以速度v做匀速圆周运动,其半径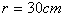 , ,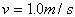 ,现将牵引的绳子迅速放长20cm,使小球在更大半径的新轨道上做匀速圆周运动,求①实现这一过渡所需的时间?②在新轨道上做匀速圆周运动时,绳子对小球的牵引力F2是原来绳子对小球牵引力F1的多少倍? ,现将牵引的绳子迅速放长20cm,使小球在更大半径的新轨道上做匀速圆周运动,求①实现这一过渡所需的时间?②在新轨道上做匀速圆周运动时,绳子对小球的牵引力F2是原来绳子对小球牵引力F1的多少倍?
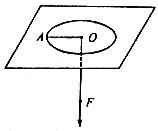
图3
解析:当绳子放长后,牵引力迅速变为O,球沿切线方向做匀速直线运动,在绳长50cm处被拉紧时,速度的方向突然发生改变后,才能沿新轨道圆做匀速圆周运动,此过程有动能损失。如果忽视这一瞬间的速度分解的关键处理方法,认为速率不变的进入新的圆周运动,导致题错解。
假设球运动到A点时开始放长,可转化成直视平面图4,①球从A点沿切线方向AB飞出,并做匀速直线运动,再被拉紧时在B点,OB为新轨道圆的半径,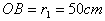 , ,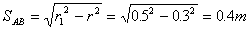 , ,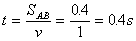 。 。
②球在B点被拉紧前的瞬间速度沿AB方向,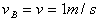 ,即拉紧后在新圆周上的匀速圆周运动的线速度为v1,二者不相等。按照vB的运动效果并作为合速度正交分解,分速度分别是:新圆上过B点沿半径OB向外的速度v2和过B点的切线方向的速度为v1,如图4所示。 ,即拉紧后在新圆周上的匀速圆周运动的线速度为v1,二者不相等。按照vB的运动效果并作为合速度正交分解,分速度分别是:新圆上过B点沿半径OB向外的速度v2和过B点的切线方向的速度为v1,如图4所示。
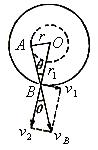
图4
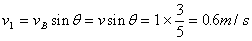 ,v2被绳子的拉力作用瞬间变为O,半径为r的圆周上运动时向心力 ,v2被绳子的拉力作用瞬间变为O,半径为r的圆周上运动时向心力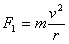 ,半径为r1的一个圆周上运动时的向心力 ,半径为r1的一个圆周上运动时的向心力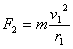 , ,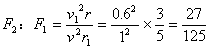
|

